悬臂梁是工程结构中常见的构件,一端固定、另一端自由,常用于模拟桥梁、阳台、机械臂等结构,在ANSYS中进行悬臂梁的静力分析时,可通过命令流实现参数化建模、网格划分、边界约束和求解后处理的全流程,以下详细介绍悬臂梁ANSYS命令流的关键步骤及代码示例。
进入ANSYS APDL环境,通过/FILNAME, Cantilever_Beam定义工作文件名,/TITLE, Static Analysis of Cantilever Beam,/PREP7进入前处理模块,材料属性定义是第一步,假设悬臂梁为钢材,弹性模量E=2.1e11 Pa,泊松比μ=0.3,密度ρ=7850 kg/m³,命令流为:
MP, EX, 1, 2.1e11
MP, PRXY, 1, 0.3
MP, DENS, 1, 7850
接下来是几何建模,悬臂梁通常简化为矩形截面,长度L=1m,截面宽度b=0.05m,高度h=0.1m,通过关键点创建线:
K, 1, 0, 0, 0 ! 定义起点关键点
K, 2, L, 0, 0 ! 定义终点关键点
L, 1, 2 ! 通过关键点生成线
RECTNG, 0, b, 0, h ! 创建矩形截面(若需3D模型可拉伸)
网格划分是影响精度的关键步骤,选择梁单元类型,如BEAM188(适合3D梁分析):
ET, 1, BEAM188
SECTYPE, 1, BEAM, RECT, , 0 ! 定义矩形截面
SECDATA, b, h, 0, 0, 0, 0, 0, 0, 0, 0 ! 截面尺寸参数
设置网格尺寸并划分网格:
LESIZE, ALL, 0.1, , , , , 1 ! 单元长度0.1m
LMESH, ALL ! 对所有线划分网格
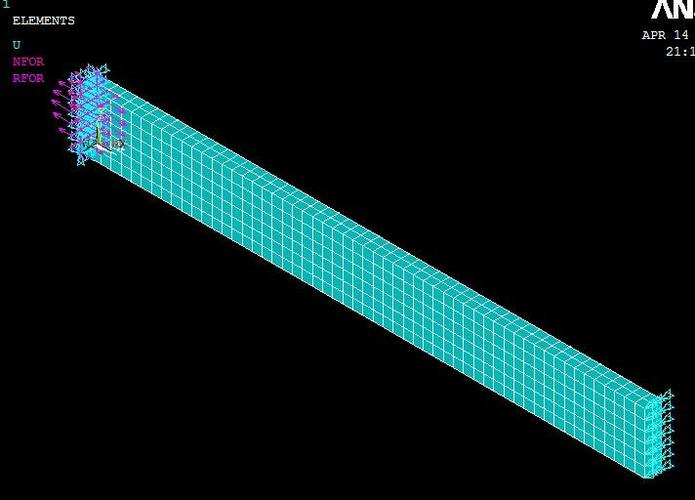
边界约束与载荷施加是悬臂梁分析的核心,固定端(x=0处)需约束所有自由度,自由端施加集中力或均布载荷,在自由端施加垂直向下的集中力F=1000N:
DK, 1, ALL, 0 ! 约束起点所有自由度
F, 2, FY, -1000 ! 在终点施加Y向力
进入求解模块/SOLU,设置分析类型为静力分析并求解:
ANTYPE, STATIC
SOLVE
后处理阶段提取关键结果,通过/POST1进入通用后处理器,查看变形和应力:
PLDISP ! 显示变形云图
ETABLE, STRESS, SMISC, 1 ! 提取弯曲应力
PLETAB, STRESS ! 显示应力云图
若需提取关键数据,可通过如下命令获取自由端挠度和最大应力:
*GET, DEF, NODE, 2, U, Y ! 获取节点2的Y向位移
*GET, MAX_STRESS, RESULT, 0, MAX ! 获取最大应力值

以下为完整命令流框架示例(部分参数需根据实际调整):
/FILNAME, Cantilever_Beam Static Analysis of Cantilever Beam
/PREP7
! 材料属性
MP, EX, 1, 2.1e11
MP, PRXY, 1, 0.3
MP, DENS, 1, 7850
! 几何建模
L, 1, 2
! 网格划分
ET, 1, BEAM188
SECTYPE, 1, BEAM, RECT
SECDATA, 0.05, 0.1
LESIZE, ALL, 0.1
LMESH, ALL
! 约束与载荷
DK, 1, ALL, 0
F, 2, FY, -1000
/SOLU
ANTYPE, STATIC
SOLVE
/POST1
PLDISP FAQs
-
如何验证悬臂梁分析结果的正确性?
可通过理论公式对比验证,自由端受集中力F时,挠度理论值为δ=FL³/(3EI),最大应力σ_max=FL/W(W为截面抗弯模量),若ANSYS结果与理论值误差在5%以内,则认为模型合理,需检查网格密度(如加密网格观察结果收敛性)、边界约束是否准确模拟固定端(如约束所有自由度而非仅平动)以及载荷施加位置是否正确。 -
悬臂梁分析中如何选择合适的单元类型?
对于细长梁(长高比>10),BEAM188或BEAM189单元效率较高,能准确模拟弯曲和剪切变形;若需考虑局部应力集中(如截面突变处),可采用SOLID185实体单元并细化网格,对于复合材料梁,可使用SHELL181层合壳单元,选择单元时需权衡计算精度与效率,例如BEAM188适合快速分析,而实体单元适合复杂几何或非线性分析。