要分辨混合运算的结果是否正确,需要遵循一定的运算规则、掌握检验方法,并具备清晰的逻辑思维能力,混合运算涉及加减乘除等多种运算,运算顺序和步骤的准确性直接影响最终结果,因此需要从多个维度进行验证和判断。

明确运算顺序是基础
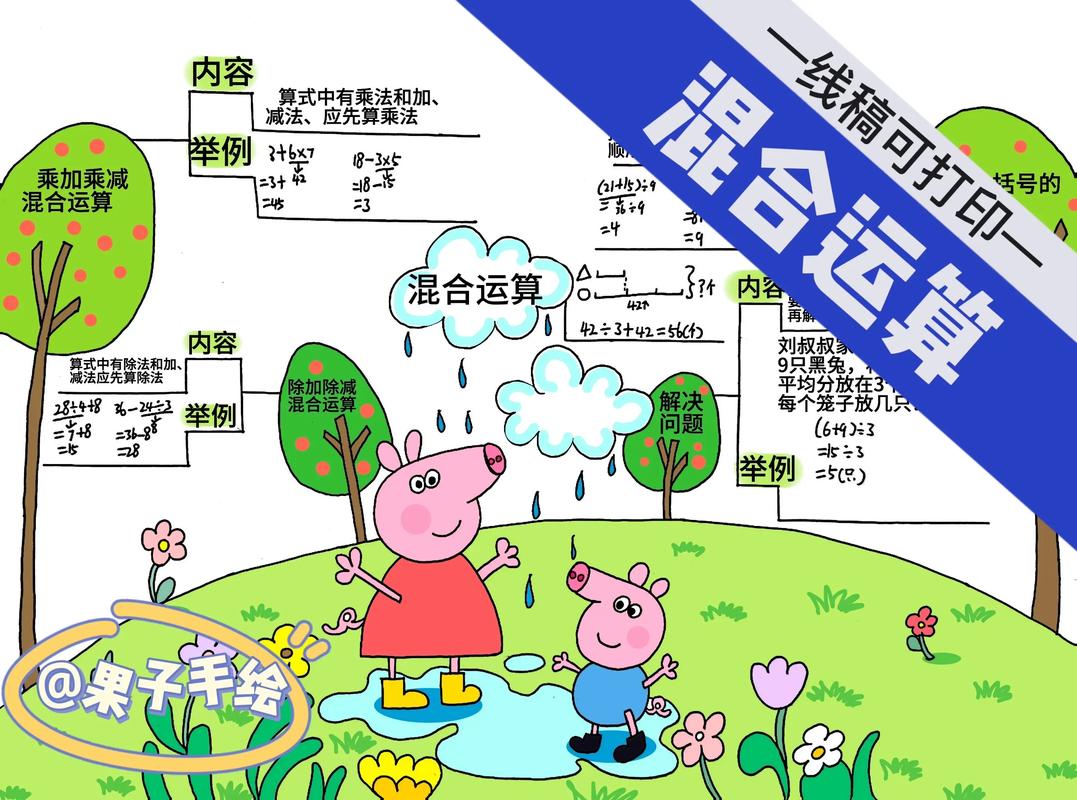
混合运算的核心在于运算顺序的正确性,数学中规定了“先乘除后加减,同级运算从左到右,有括号先算括号内”的规则,在计算前,首先要观察算式结构,确定运算顺序,对于算式“3 + 5 × 2”,应先算乘法“5 × 2 = 10”,再算加法“3 + 10 = 13”,而非从左到右依次计算得到“8 × 2 = 16”,如果算式包含括号,如“(3 + 5) × 2”,则需先算括号内的“3 + 5 = 8”,再算乘法“8 × 2 = 16”,运算顺序错误会导致整个结果偏差,因此第一步必须严格检查是否符合规则。
分步计算与逐步验证
在复杂的混合运算中,建议将整个算式拆分为多个步骤,逐步计算并记录中间结果,便于回查,计算“12 - 4 × (6 ÷ 2) + 3”时,可分步进行:
- 先算括号内的除法:“6 ÷ 2 = 3”,算式变为“12 - 4 × 3 + 3”;
- 再算乘法:“4 × 3 = 12”,算式变为“12 - 12 + 3”;
- 最后算加减法(从左到右):“12 - 12 = 0”,“0 + 3 = 3”。
每一步计算后,立即检查中间结果是否正确,如“4 × 3”是否等于12,“12 - 12”是否为0,避免错误累积到最终结果,若某一步骤结果异常,需及时重新计算该步骤,确保每一步的准确性。
运用逆运算进行检验
逆运算是验证混合运算结果的有效方法,加法的逆运算是减法,乘法的逆运算是除法,通过将最终结果作为已知条件,反向推导原算式是否成立,若计算“25 ÷ 5 + 3 × 2”得到“5 + 6 = 11”,可通过逆运算验证:
- 从11出发,减去“3 × 2 = 6”,得到“11 - 6 = 5”;
- 再将5乘以5,得到“5 × 5 = 25”,与原算式中的被除数一致,说明结果正确。
对于含括号的算式,如“(10 + 2) × 3 - 8 = 36”,可先算“36 + 8 = 44”,再“44 ÷ 3 ≈ 14.666”,与“10 + 2 = 12”不符,此时需检查原计算步骤,可能是“(10 + 2) × 3 = 36”后,“36 - 8 = 28”,逆运算“28 + 8 = 36”,“36 ÷ 3 = 12”,与“10 + 2”一致,说明正确结果应为28而非36,逆运算能有效暴露计算过程中的逻辑错误。
关注符号与运算细节
混合运算中,符号和运算细节的疏漏是常见错误来源,负号的处理:“-2 × 3 + 4”应先算乘法“-2 × 3 = -6”,再算加法“-6 + 4 = -2”,而非忽略负号直接计算“2 × 3 + 4 = 10”,小数、分数的运算需注意对齐数位和通分:如“0.5 × 4 + 1.2 ÷ 0.6”,应先算“0.5 × 4 = 2”,“1.2 ÷ 0.6 = 2”,再“2 + 2 = 4”;分数运算如“1/2 + 1/3 × 2”,需先算乘法“1/3 × 2 = 2/3”,再通分加法“1/2 + 2/3 = 3/6 + 4/6 = 7/6”,符号和小数点的错误可能导致结果数量级偏差,需重点检查。
借助工具与对比分析
在复杂运算中,可借助计算器等工具进行辅助验证,但需注意手动计算与工具计算的一致性,计算“100 - 20 × (3 + 2) ÷ 5”,手动步骤为:1. 括号内“3 + 2 = 5”;2. 乘法“20 × 5 = 100”;3. 除法“100 ÷ 5 = 20”;4. 减法“100 - 20 = 80”,用计算器输入相同算式,若结果一致,则可信;若不一致,需检查计算器输入是否正确(如括号是否遗漏),或手动计算是否有误,对于同一算式,可采用不同计算顺序(如拆分括号、提取公因数)对比结果,25 × 4 + 25 × 6”可通过“25 × (4 + 6) = 25 × 10 = 250”验证,若直接计算“25 × 4 = 100”,“25 × 6 = 150”,“100 + 150 = 250”,结果一致,说明正确。
常见错误类型与规避
分辨结果时,需警惕常见错误类型:
- 运算顺序错误:如“10 + 5 ÷ 5”误算为“(10 + 5) ÷ 5 = 3”,正确应为“10 + 1 = 11”;
- 符号遗漏:如“-3 + 2 × 3”误算为“-3 + 6 = 3”(正确),但若误写为“3 + 2 × 3 = 9”则错误;
- 括号处理不当:如“2 × (3 + 4) - 5”误算为“2 × 3 + 4 - 5 = 5”,正确应为“2 × 7 - 5 = 9”;
- 小数/分数运算错误:如“0.1 × 0.1 + 0.9”误算为“0.01 + 0.9 = 0.91”,正确无误,但“1/2 ÷ 1/4”易误算为“1/8”,正确应为“2”。
规避错误的关键是:计算前先标记运算顺序,计算中每一步书写清晰,计算后通过逆运算或工具验证,尤其注意符号、括号和特殊数值的处理。
实际应用中的结果分辨
在实际问题中,混合运算的结果需结合题意合理性判断。“一件商品原价100元,先打8折再减20元,现价多少?”算式为“100 × 0.8 - 20 = 80 - 20 = 60”,若结果为“100 × 0.8 + 20 = 100”,明显不符合促销逻辑,需检查运算符号是否正确,又如“班级有40人,男生占60%,女生中50%参加兴趣小组,参加兴趣小组的女生有多少人?”算式为“40 × (1 - 60%) × 50% = 40 × 0.4 × 0.5 = 8”,若结果为“40 × 60% × 50% = 12”,则错误地将女生比例误算为男生比例,需重新审视题意与算式的对应关系。

相关问答FAQs
问题1:混合运算中,如果括号内外都有乘除法,应该如何确定运算顺序?
解答:根据运算规则,无论括号内外,乘除法属于同级运算,应按照从左到右的顺序计算,例如算式“10 × 2 ÷ (5 × 4) ÷ 2”,需先算括号内“5 × 4 = 20”,算式变为“10 × 2 ÷ 20 ÷ 2”,然后从左到右依次计算:“10 × 2 = 20”,“20 ÷ 20 = 1”,“1 ÷ 2 = 0.5”,若误将括号外的乘除法随意调整顺序,如先算“2 ÷ 2 = 1”,再算“10 × 1 ÷ 20 = 0.5”,虽然结果巧合一致,但逻辑错误,复杂算式中可能导致偏差,必须严格遵循从左到右原则。
问题2:如何快速判断混合运算结果的数量级是否合理?
解答:通过估算和数量级分析可快速判断结果合理性,123 × 4 + 567 ÷ 7”,估算“123 × 4 ≈ 120 × 4 = 480”,“567 ÷ 7 ≈ 560 ÷ 7 = 80”,总和约“480 + 80 = 560”,若实际结果为“492 + 81 = 573”,与估算接近,合理;若结果为“492 + 8 = 500”,则“567 ÷ 7”明显估算错误,需检查除法步骤,再如“0.05 × 20 - 0.1”,估算“0.05 × 20 = 1”,“1 - 0.1 = 0.9”,若结果为“10”或“0.01”,则数量级偏差过大,需重新检查小数点位置或运算符号,估算虽不精确,但能有效暴露明显错误。