distance 命令在不同的系统和软件中含义不同,但核心思想都是计算“距离”,这个“距离”可以是:
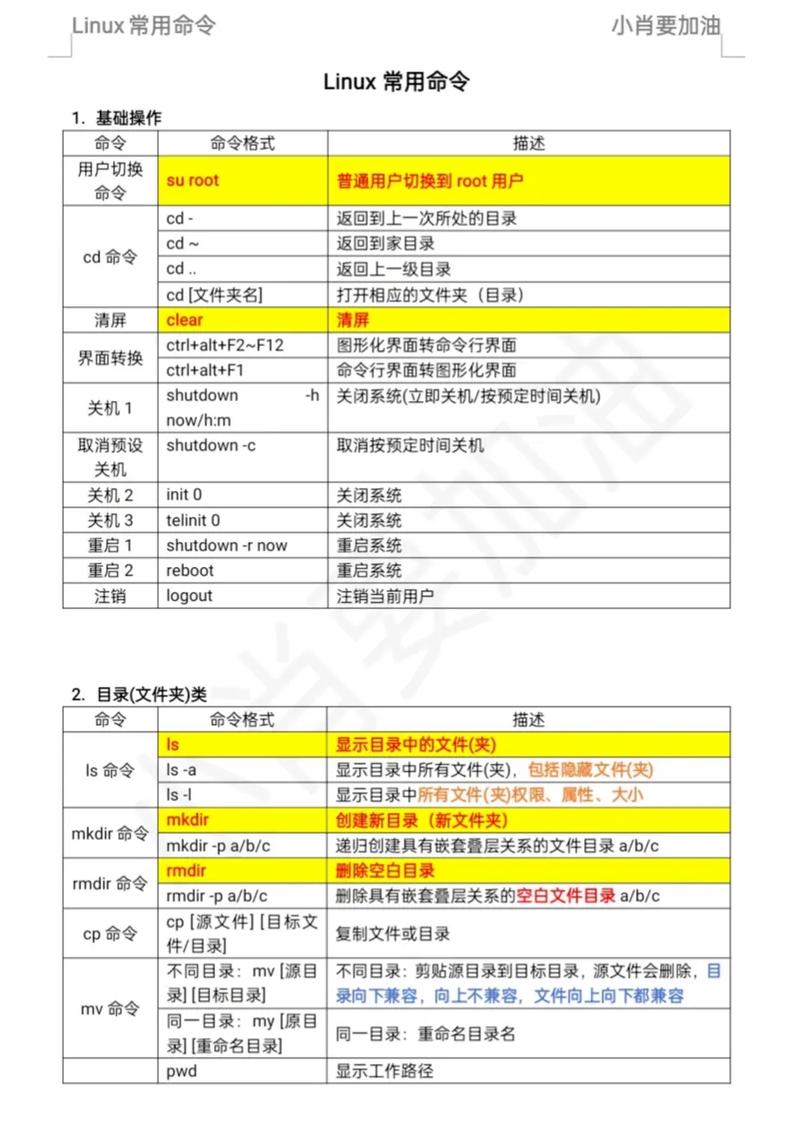
- 地理空间距离:两个经纬度坐标之间的实际距离。
- 数据相似度距离:在数据科学和机器学习中,衡量两个数据点向量之间的“差异”或“不相似度”。
下面我将分别介绍在 网络工具 和 数据科学工具 中的 distance 命令。
网络工具中的 distance (网络诊断)
在网络诊断领域,distance 命令通常不是一个独立的、通用的命令,它的功能被集成在更常用的命令中,最典型的是 traceroute (在 Windows 中是 tracert)。
traceroute 的作用是显示数据包从你的计算机到目标主机所经过的路由节点(网关),这个路径上的“跳数”(Hop Count)可以被看作是一种“距离”——即数据包需要跨越多少个网络设备才能到达目的地。
traceroute / tracert 的工作原理
它会发送一系列数据包,并逐步增加“生存时间”(TTL, Time To Live)值:
- 第一跳:发送一个 TTL=1 的数据包,第一个路由器收到后,会将 TTL 减到 0,然后丢弃该数据包,并向源主机发送一个“超时”消息,这样我们就知道了第一个路由器的 IP 和响应时间。
- 第二跳:发送一个 TTL=2 的数据包,第一个路由器将 TTL 减到 1 后转发给第二个路由器,第二个路由器再将 TTL 减到 0,并返回“超时”消息,这样我们就知道了第二个路由器的信息。
- 以此类推,直到数据包到达最终目的地。
如何使用
在 Linux 或 macOS 上:
traceroute [目标域名或IP地址]
示例:
traceroute google.com
输出示例解读:
traceroute to google.com (142.250.199.100), 30 hops max, 60 byte packets
1 gateway (192.168.1.1) 2.343 ms 1.876 ms 1.912 ms <-- 第一跳(你的路由器)
2 isp-core-router-1 (203.0.113.10) 15.234 ms 14.567 ms 16.789 ms <-- 第二跳(你的ISP核心路由器)
3 ... (中间可能有多跳) ...
10 * * * <-- 某些路由器可能不响应
11 142.250.199.100 (142.250.199.100) 45.123 ms 44.567 ms 45.234 ms <-- 最后一跳(Google的服务器)这里的“跳数”就是网络距离。

在 Windows 上:
tracert [目标域名或IP地址]
示例:
tracert google.com
输出格式略有不同,但原理和提供的信息(跳数、IP、响应时间)是完全一样的。
数据科学和编程中的 distance
在 Python (特别是 scipy 和 sklearn 库) 或 R 语言中,distance 是一个非常重要的概念,用于衡量数据点之间的相似性,距离越小,代表数据点越相似。
常见的距离度量
-
欧几里得距离
- 概念:我们日常生活中理解的“直线距离”,在二维平面上,就是两点之间的线段长度。
- 适用场景:连续型数据,且各维度量纲相似。
- 公式:
d = sqrt((x2-x1)² + (y2-y1)² + ...)
-
曼哈顿距离
- 概念:在网格状路径(像在曼哈顿的街道上开车)上,从一个点走到另一个点的最短路径长度,只计算坐标轴方向的差值之和。
- 适用场景:数据具有网格状特征,或者当需要避免欧氏距离中对大差值的过度放大时。
- 公式:
d = |x2-x1| + |y2-y1| + ...
-
余弦相似度 / 余弦距离
- 概念:衡量两个向量方向上的一致性,而不是它们的大小,值域在 [-1, 1] 之间,1 表示方向完全相同,-1 表示方向完全相反,0 表示正交(无关)。
- 适用场景:文本分析(如 TF-IDF 向量)、推荐系统,关心“内容”相似性而非“数量”相似性。
- 距离转换:
Cosine Distance = 1 - Cosine Similarity
Python 中的 distance 计算
Python 的科学计算库提供了丰富的工具。
使用 scipy.spatial.distance
from scipy.spatial import distance
import numpy as np
# 定义两个点(向量)
point_a = np.array([1, 2, 3])
point_b = np.array([4, 5, 6])
# 1. 欧几里得距离 (默认)
euclidean_dist = distance.euclidean(point_a, point_b)
print(f"欧几里得距离: {euclidean_dist:.4f}") # 输出: 5.1962
# 2. 曼哈顿距离
manhattan_dist = distance.cityblock(point_a, point_b)
print(f"曼哈顿距离: {manhattan_dist}") # 输出: 9
# 3. 余弦距离
cosine_dist = distance.cosine(point_a, point_b)
print(f"余弦距离: {cosine_dist:.4f}") # 输出: 0.0254
# 4. 计算一个点到多个点的距离
points_c = np.array([[7, 8, 9], [10, 11, 12]])
# cdist 计算点a到points_c中每个点的距离
distances_to_c = distance.cdist([point_a], points_c, 'euclidean')
print(f"点A到点集C的距离:\n{distances_to_c}")
# 输出:
# [[10.3923 15.5885]]
使用 scikit-learn
在机器学习中,sklearn 的 metrics 模块也提供了距离计算功能,常用于评估聚类算法。
from sklearn.metrics import pairwise_distances
# 一组数据点
data = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
# 计算所有点对之间的欧几里得距离矩阵
distance_matrix = pairwise_distances(data, metric='euclidean')
print("距离矩阵:")
print(distance_matrix)
# 输出:
# [[0. 2.82842712 5.65685425 8.48528137]
# [2.82842712 0. 2.82842712 5.65685425]
# [5.65685425 2.82842712 0. 2.82842712]
# [8.48528137 5.65685425 2.82842712 0. ]]
| 领域 | 命令/工具 | 核心概念 | 主要用途 |
|---|---|---|---|
| 网络诊断 | traceroute / tracert |
跳数 | 诊断网络连接问题,显示数据包的传输路径,判断延迟和丢包位置。 |
| 数据科学 | scipy.spatial.distancesklearn.metrics |
向量差异 | 衡量数据点之间的相似性,用于聚类、分类、推荐系统、异常检测等机器学习任务。 |
当您提到 distance 命令时,需要根据上下文来判断它具体指的是哪种“距离”,在日常网络排查中,它通常指 traceroute 的路径长度;而在数据分析中,它则指代数学上的向量距离度量。