CAD中的蒙版命令是一项非常实用的功能,主要用于控制图形的显示区域，隐藏不需要的部分，使图纸更加清晰、整洁，在AutoCAD中，蒙版功能主要通过“WIPEOUT”命令实现，它可以在当前图层上创建一个空白区域，覆盖下面的对象，从而达到遮挡效果，与传统的“块”或“图层冻结”相比，蒙版不会真正删除或修改对象，只是视觉上的隐藏，便于编辑和修改，下面将详细介绍CAD蒙版命令的使用方法、技巧及注意事项。

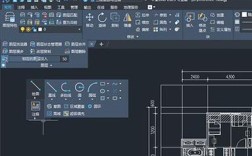
执行“WIPEOUT”命令的方式有多种：可以通过命令行直接输入“WIPEOUT”并按回车键，或在功能区“注释”选项卡的“标注”面板中找到“遮罩”按钮，也可以通过快捷键“W”快速调用，执行命令后，命令行会提示用户选择“多段线”或“[多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多段线(P)/多边形(P)/多