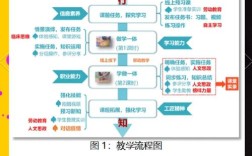
在解决应用题时,寻找合适的解法往往是关键步骤,这需要系统性的思维方法和多角度的分析技巧,理解题意是基础,需要仔细阅读题目,明确已知条件、未知量以及问题要求,必要时可以通过画图、列表等方式将抽象信息转化为直观形式,在行程问题中,可以画出路线示意图;在工程问题中,可以用表格列出各部分的工作量和效率,这一步的核心是避免遗漏关键信息,同时识别题目中的隐含条件,相遇”“追及”“完成”等词语背后对应的数学关系。

分析数量关系是核心环节,需要根据题目类型,联想相关的公式和模型,例如行程问题中的路程=速度×时间,工程问题中的工作量=效率×时间,利润问题中的利润=售价-成本等,对于复杂的应用题,可能需要拆解问题,将其转化为若干个简单的小问题,逐步解决,逆向思维和正向推理可以结合使用:从问题出发,思考需要哪些中间量才能求解;从已知条件出发,思考可以推导出哪些新的结论,在涉及多个变量的题目中,可以设未知数,并根据等量关系列出方程或方程组,这是代数方法中常用的策略。
选择合适的解题方法也是重要一环,常见的方法包括算术法、代数法、图解法、假设法、枚举法等,算术法适合简单问题,通过四则运算直接求解;代数法通过设未知数、列方程来解决问题,尤其适合复杂的关系;图解法可以通过线段图、示意图等直观展示数量关系,帮助理解;假设法通过设定某个条件的极端情况来简化问题,鸡兔同笼”问题;枚举法则适用于有限种可能的题目,通过逐一尝试找到答案,选择哪种方法取决于题目特点和自身思维习惯,有时需要多种方法结合使用。
在解题过程中,验证和反思是确保答案正确性的关键,得到结果后,需要将其代入原题进行检验,看是否符合所有条件;思考是否有更简便的解法,总结解题规律和经验,在解决比例问题时,可以通过验证比例的一致性来检查答案的合理性;在解决最优化问题时,可以通过比较不同方案的结果来确认最优解,积累常见题型和解题模型也至关重要,通过大量练习,熟悉各类问题的特征和解题套路,可以提高解题效率和准确性。
为了更直观地展示不同类型应用题的解题思路,以下通过表格列举几类常见问题的核心方法和示例: 类型 | 核心关系式 | 常用方法 | 示例简述 | |----------------|--------------------------|------------------------|------------------------------| | 行程问题 | 路程=速度×时间 | 线段图、方程法 | 相遇问题:两者路程和=总路程 | | 工程问题 | 工作量=效率×时间 | 单位“1”设定、比例法 | 合作问题:合作效率=效率和 | | 利润问题 | 利润=售价-成本,利润率=利润/成本 | 方程法、列表分析法 | 定价问题:根据利润率求售价 | | 浓度问题 | 溶质质量=溶液质量×浓度 | 十字交叉法、方程法 | 稀释问题:溶质质量不变 | | 不等式应用题 | 根据题意列不等式(组) | 数轴法、转化法 | 方案设计问题:求最优解范围 |

在实际解题中,可能会遇到题目条件隐蔽、关系复杂的情况,此时需要灵活转换思路,在涉及多个比例的问题中,可以通过设定比例系数来简化计算;在动态变化的问题中,可以抓住不变量(如总量、差量)作为突破口,注意单位的统一和术语的准确理解,避免因概念混淆导致错误。“增加了”和“增加到”、“倍数”和“分数”等词语的含义需要严格区分。
对于学生而言,建立错题本并定期回顾是提升应用题解题能力的有效途径,通过分析错误原因,是概念不清、关系分析错误还是计算失误,可以有针对性地进行强化训练,多与他人交流解题思路,学习不同的思维方式,也能拓宽解题思路,同一道题可能有多种解法,通过比较不同解法的优劣,可以优化自己的解题策略。
相关问答FAQs:
-
问:遇到复杂的应用题时,如何快速找到解题突破口?
答:快速找到解题突破口的关键是“抓关键信息”和“找不变量”,首先通读题目,标记出已知量、未知量和问题目标,重点关注题目中的“不变量”“等量关系”或“比例关系”,在浓度问题中,溶质质量往往是不变量;在行程问题中,若速度不变,则路程与时间成正比,尝试将复杂问题拆解为简单子问题,或从问题倒推,思考需要哪些条件才能求解,逐步缩小范围,联想该题型的常见模型(如工程问题中的“单位1”模型),用对应的方法尝试转化问题,通常能快速找到突破口。 (图片来源网络,侵删)
(图片来源网络,侵删) -
问:如何判断应用题是否需要用方程解决?什么情况下适合算术法?
答:判断是否用方程主要看题目中的数量关系是否复杂、未知量是否较多,当题目中涉及多个未知量,且它们之间存在等量关系(如和、差、倍数关系),或问题需要逆向求解(如已知结果求某个条件)时,用方程法更直观,通过设未知数、列方程可以系统性地表达关系,而算术法适合数量关系简单、未知量较少的题目,尤其是可以通过直接运算(如加减乘除、比例分配)解决的问题,已知两个数的和与差,求这两个数”用算术法中的“和差公式”更快捷,算术法依赖思维技巧,方程法更普适,对于初学者,方程法更容易掌握,而算术法需要一定练习才能灵活运用。