数形结合思想是数学教学中的重要方法论,它通过将抽象的数学语言与直观的图形、图像相结合,帮助学生降低理解难度,提升分析问题和解决问题的能力,在教学中有效导入数形结合思想,需要遵循学生的认知规律,通过分层设计、情境创设和实践活动,逐步引导学生从“形”感知“数”,从“数”推导“形”,最终实现两者灵活转化,以下从理论基础、导入策略、实施步骤和案例分析四个方面展开详细说明。

数形结合思想的理论基础与教学价值
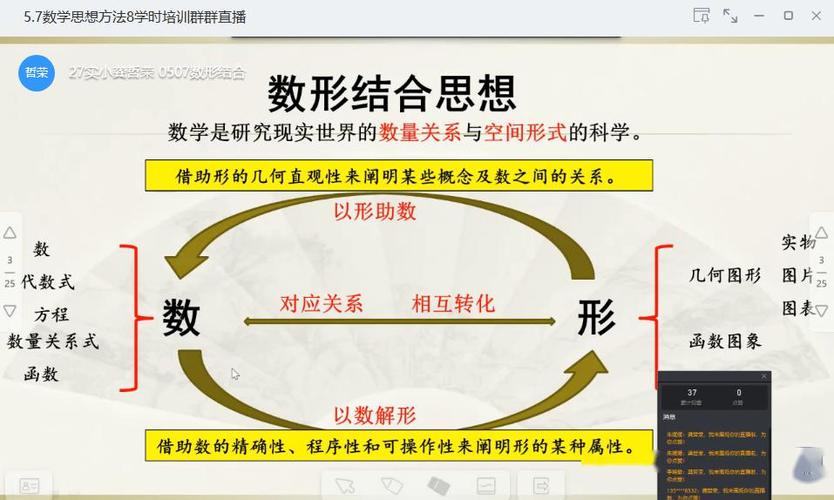
数形结合的核心是“以形助数”和“以数解形”,前者利用图形的直观性揭示数量关系,例如用数轴理解相反数、绝对值的概念;后者通过代数运算精确描述图形性质,例如用坐标法证明几何问题,从认知心理学角度看,青少年的思维发展正处于从具体形象思维向抽象逻辑思维过渡的关键期,数形结合恰好契合这一特点:图形为抽象数学提供了“脚手架”,使复杂问题可视化、简单化,在函数教学中,单调性与图像升降的对应关系,能帮助学生快速理解导数的几何意义,数形结合还能培养学生的空间想象能力和逻辑推理能力,为后续学习解析几何、微积分等内容奠定基础。
数形结合思想的导入策略
分阶段渗透,循序渐进
数形结合的导入需遵循“感知—理解—应用”的阶梯式路径。
- 低年级阶段(小学1-3年级):侧重实物与图形的直观对应,用小棒摆数字“5”,通过图形的拆分与组合理解加减法;用长方形面积模型讲解乘法分配律(如(a+b)×c=a×c+b×c)。
- 中年级阶段(小学4-6年级):引入简单图表与数轴,用折线统计图分析数据变化,用数轴比较分数大小,通过几何图形的分割理解分数的加减法。
- 高年级及以上:强化坐标思想与函数图像,在初中阶段用坐标系确定点的位置,通过一次函数图像理解k、b的几何意义;在高中阶段用向量坐标解决几何问题,用导数图像研究函数极值。
创设问题情境,激发转化意识
情境化教学是导入数形结合的有效途径,教师可设计“数”与“形”冲突的问题,引导学生主动寻找转化方法,在“鸡兔同笼”问题中,学生既可通过代数方程求解,也可用画图法(假设全是鸡,再替换兔子)直观展示数量关系,通过对比两种方法的优劣,学生能体会到“形”的直观性和“数”的精确性,从而主动构建数形转化的思维习惯。
利用信息技术,实现动态数形结合
借助几何画板、Desmos等动态数学软件,可让“数”与“形”的互动更加生动,在二次函数y=ax²+bx+c的教学中,学生通过拖动参数a、b、c的滑块,实时观察图像开口方向、顶点位置的变化,直观理解参数对函数图像的影响,这种动态演示能帮助学生建立“数”变“形”变的关联,突破静态图形的局限性。
数形结合思想的具体实施步骤
分析问题,明确“数”与“形”的切入点
引导学生先判断问题的核心:若涉及数量关系或抽象运算,可尝试用图形辅助理解(如用韦恩图解决集合问题);若涉及几何图形的位置或性质,可尝试用代数方法量化描述(如用距离公式证明三角形全等),在“求|x-1|+|x-3|的最小值”问题中,学生可通过画数轴,将绝对值转化为点到点的距离,直观发现最小值为2。
构建图形,提炼数学特征
在“以形助数”时,需确保图形准确反映数量关系,用函数图像解不等式ax²+bx+c>0时,需先准确画出抛物线,标注与x轴的交点,再根据开口方向确定解集,教师应强调图形的规范性,避免因图形失真导致误解。
数形互译,验证结论
引导学生通过“数”与“形”的相互验证,确保结论的准确性,在“证明勾股定理”时,既可以通过代数运算(如面积法)证明a²+b²=c²,也可以通过几何图形(如赵爽弦图)的拼接直观展示面积关系,通过双向验证,学生能深刻体会数形结合的严谨性。
总结归纳,提炼思想方法
在应用数形结合解决问题后,需引导学生归纳其适用场景和转化技巧,哪些问题适合用数轴(如比较数的大小、解绝对值不等式),哪些问题适合用坐标系(如求两点距离、直线斜率),通过总结,帮助学生形成系统的数形结合思维框架。

数形结合思想的教学案例分析
案例:初中数学“一元二次方程根的分布”教学
- 问题:已知方程x²-2x+m=0有两个不相等的实数根,求m的取值范围。
- 数形结合导入:
- 以形助数:引导学生画出函数y=x²-2x+m的图像(抛物线),标出对称轴x=1及顶点纵坐标y=m-1。
- 条件转化:根据“有两个不相等实数根”,转化为“抛物线与x轴有两个交点”,即判别式Δ=4-4m>0,且顶点在x轴下方(m-1<0)。
- 数形验证:通过图像直观发现,当m<1时,抛物线与x轴有两个交点,与代数结果一致。
- 教学效果:学生通过图像与代数条件的结合,不仅掌握了m<1的结论,还理解了判别式、顶点坐标与根的分布的关联,提升了综合分析能力。
数形结合思想的教学注意事项
- 避免形式化:数形结合需服务于问题解决,而非为了“画图”而画图,简单计算题无需过度依赖图形,以免增加认知负担。
- 强调图形准确性:错误的图形会导致错误结论,教师需规范作图步骤,培养学生严谨的绘图习惯。
- 鼓励个性化转化:同一问题可能有多种数形结合方法,应鼓励学生尝试不同思路,如用面积法、向量法等解决几何问题,培养发散思维。
相关问答FAQs
问题1:如何判断一道题是否适合用数形结合思想解决?
解答:判断标准主要有三点:一是问题中是否包含抽象的数量关系(如绝对值、不等式、函数等),可通过图形直观化;二是问题是否涉及几何图形的位置、性质或变换,可通过代数方法量化;三是“数”与“形”是否能相互验证,例如代数结果与图形特征是否一致,在“求函数f(x)=|x-2|+|x+3|的最小值”中,绝对值表达式可通过数轴转化为距离问题,此时数形结合能显著简化求解过程。
问题2:学生在数形结合转换中常出现哪些误区?如何纠正?
解答:常见误区包括:一是图形与代数条件脱节,如画函数图像时忽略定义域限制,导致结论错误;二是过度依赖图形而忽略代数验证,例如仅通过观察图像判断根的个数,未计算判别式;三是混淆“形”的直观性与“数”的精确性,如用草图代替精确作图得出错误结论,纠正方法:一是强化“数形互译”训练,要求学生每一步图形转化都对应代数条件;二是通过反例教学,展示图形失真导致的错误,培养严谨性;三是鼓励学生用多种方法交叉验证,如代数法与几何法结合解决问题,避免单一思维局限。


