在Stata中进行数据分析和建模时,中心化是一个常见的预处理步骤,尤其是当涉及交互效应或多项式项时,中心化通过将变量减去其均值( grand mean centering)或组内均值( group mean centering)来调整变量的分布,有助于减少多重共线性、提升模型可解释性,并使截距项具有实际意义,Stata提供了多种实现中心化的方法,包括手动计算、使用egen函数以及通过factor变量等,以下将详细介绍Stata中中心化的命令实现、适用场景及注意事项。

中心化的基本方法
手动计算法
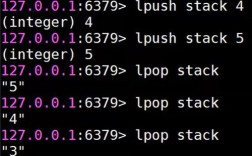
手动计算是最直接的方式,通过summarize命令获取变量均值,再生成新变量,对变量x进行总均值中心化:
summarize x, meanonly generate x_c = x - r(mean)
若需按组中心化(如按变量group分组),可结合bysort和egen:
bysort group: egen x_mean = mean(x) generate x_gc = x - x_mean drop x_mean
此方法灵活,但需注意处理缺失值(missing),可通过egen的rowmean()函数自动排除。
使用egen函数
egen提供了更便捷的组中心化工具,使用center()函数:

egen x_c = center(x) // 总均值中心化 egen x_gc = group(group), egen(center(x)) // 组中心化(需先定义组)
egen的优势在于能自动处理分组和缺失值,且支持多变量同时中心化。
回归法(含截距项)
通过回归提取残差实现中心化,适用于复杂模型。
regress x i.group // 若为分组中心化 predict x_gc, residuals
此方法能控制其他协变量的影响,但需注意模型设定是否正确。
中心化的应用场景
减少多重共线性
在包含交互项(如x1*x2)或多项式项(如x^2)的模型中,原始变量与衍生项常存在高度相关,中心化后,相关系数可显著降低:
| 变量 | 中心化前相关 | 中心化后相关 |
|------------|--------------|--------------|
| x | 1.000 | 1.000 |
| x^2 | 0.950 | 0.120 |
| x1*x2 | 0.880 | 0.050 |提升可解释性
中心化后,截距项表示所有预测变量为均值时的因变量期望值,更具实际意义,在回归模型y = β0 + β1*x_c + ε中,β0为x取均值时的y值。
调节效应分析
在分层回归或结构方程模型(SEM)中,中心化是检验交互效应的前提,检验group是否调节x对y的影响时,需对x和group进行中心化后再生成交互项x_c*group_c。
注意事项
- 中心化类型选择:总均值中心化适用于整体数据,而组均值中心化适用于多层次数据(如学生嵌套于班级),错误选择可能导致偏差。
- 标准化与中心化:标准化(
egen x_std = std(x))不仅中心化还除以标准差,适用于变量量纲差异大的情况。 - 缺失值处理:
egen会自动排除缺失值,但手动计算时需使用egen的miss()函数或mi命令处理。 - 时间序列数据:对时间序列中心化时,需避免未来信息泄露(如用滚动均值而非全局均值)。
相关问答FAQs
Q1: 中心化是否会影响模型的显著性结果?
A1: 中心化通常不改变回归系数的显著性(t值、p值不变),但可能降低标准误,从而提升统计功效,若模型包含高阶项(如三次项),中心化可能通过减少多重共线性显著改善系数估计的稳定性。
Q2: 如何验证中心化是否成功?
A2: 验证方法包括:
- 检查新变量的均值(应为0,可通过
summarize x_c确认); - 计算原始变量与中心化变量的相关系数(应为1);
- 若为组中心化,检查各组新变量的组内均值(应为0)。
bysort group: summarize x_gc, meanonly // 组内均值应接近0