在数轴上找规律是数学学习中一项重要的技能,它不仅能培养观察力和逻辑思维,还能为后续的代数学习奠定基础,数轴上的规律通常表现为数字之间的固定关系,如等差、等比或其他更复杂的模式,掌握找规律的方法,需要从观察、分析、验证和总结四个步骤入手,逐步深入。
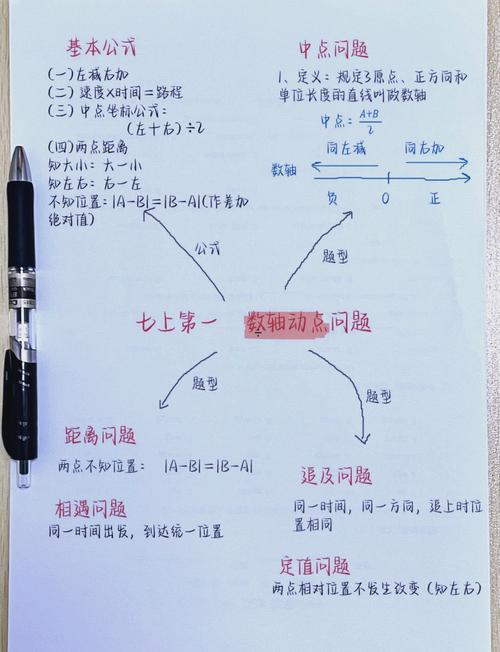
观察是找规律的第一步,我们需要仔细观察数轴上给出的数字序列,注意数字的变化趋势,数轴上依次标记着2、5、8、11、14……,这些数字呈现出递增的趋势,且相邻数字之间的差值相同(5-2=3,8-5=3,11-8=3),这种相邻两项之差相等的规律称为等差数列,公差为3,如果数字序列是2、4、8、16、32……,则呈现出递增趋势,且相邻两项的比值相等(4÷2=2,8÷4=2,16÷8=2),这种规律称为等比数列,公比为2,除了等差和等比,还可能存在其他规律,如平方数、立方数或交替变化的模式,1、4、9、16、25……是平方数序列(1²、2²、3²、4²、5²),而1、1、2、3、5、8……则是斐波那契数列,每一项都是前两项之和。
分析是找规律的核心环节,在观察的基础上,我们需要对数字之间的关系进行深入分析,可以通过计算相邻数字的差、和、积或商,来寻找隐藏的规律,对于序列3、7、13、21、31……,计算相邻两项的差:7-3=4,13-7=6,21-13=8,31-21=10,得到的差值序列是4、6、8、10……,这是一个新的等差数列,公差为2,原数列的规律是“后一项与前一项的差依次增加2”,对于更复杂的序列,可能需要多次分析或结合多种运算,序列1、3、7、15、31……,相邻两项的差是2、4、8、16……,这是一个等比数列,公比为2,因此原数列的规律是“后一项等于前一项乘以2再加1”(3=1×2+1,7=3×2+1,15=7×2+1,31=15×2+1)。
验证是确保规律正确性的关键步骤,当我们找到一个可能的规律后,需要用这个规律去预测数列中的下一个数字,并与已知的数字进行对比,如果预测正确,说明规律可能是正确的;如果预测错误,则需要重新分析,对于序列1、2、4、7、11……,相邻两项的差是1、2、3、4……,因此下一个差值应该是5,下一个数字是11+5=16,如果数列中下一个数字确实是16,那么规律成立;如果不是,则需要寻找其他规律,验证的过程可以避免因观察不全面或分析错误而得出错误的结论。
总结是找规律的最终目的,通过多次练习,我们可以总结出一些常见的规律类型和解题方法,以便在遇到类似问题时能够快速解决,等差数列和等比数列是最基本的两种规律,几乎所有数列问题都会涉及这两种模式或其变体,还可以总结出“差分法”(计算相邻项的差)、“商分法”(计算相邻项的比)、“递推法”(寻找项与项之间的递推关系)等常用方法,掌握这些方法,能够提高找规律的效率和准确性。

为了更直观地展示找规律的过程,我们可以用表格来分析一个具体的数列,数列:5、10、15、20、25……
| 序号 (n) | 数列中的数字 (aₙ) | 相邻两项的差 (aₙ - aₙ₋₁) |
|---|---|---|
| 1 | 5 | |
| 2 | 10 | 10 - 5 = 5 |
| 3 | 15 | 15 - 10 = 5 |
| 4 | 20 | 20 - 15 = 5 |
| 5 | 25 | 25 - 20 = 5 |
从表格中可以明显看出,相邻两项的差都是5,因此这是一个等差数列,公差为5,通项公式可以表示为aₙ = 5n,用这个公式验证:当n=1时,a₁=5×1=5;n=2时,a₂=5×2=10,与数列一致,说明规律正确。
在数轴上找规律需要仔细观察、深入分析、严格验证和善于总结,通过不断练习,我们可以提高自己的数学思维能力,轻松应对各种数列问题。
相关问答FAQs

问:如果数列中的数字变化没有明显的规律,应该怎么办?
答:当数列变化不明显时,可以尝试更复杂的分析方法,计算相邻数字的差、和、积或商后,观察得到的新数列是否有规律;或者尝试将数列拆分为奇数项和偶数项,分别寻找规律;还可以考虑数字的因数、倍数、平方、立方等属性,有时规律可能涉及周期性变化或递推关系,需要结合多种方法综合分析,如果仍找不到规律,可能是数列的规律较为特殊,需要跳出常规思维,尝试其他运算模式。
问:找规律时,如何判断自己找到的规律是否正确?
答:判断规律是否正确,最有效的方法是用找到的规律预测数列中的下一个数字或后续数字,然后与已知的数列进行对比,如果预测结果与实际数列一致,说明规律可能是正确的;如果预测错误,则需要重新分析,还可以用通项公式或递推关系验证数列中的已知项,确保所有项都符合规律,对于复杂的数列,可能需要多次验证,确保规律在所有情况下都成立。