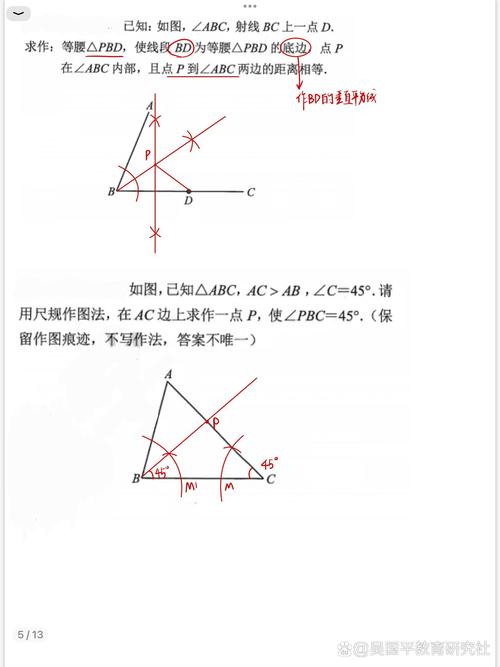
尺规作图作为古希腊几何学的重要基础,不仅限于图形的绘制,其核心逻辑蕴含着对数量关系的直观表达,在尺规作图中,线段的长度被用来表示数值,而通过线段的加减操作,即可实现数学中加法与减法的可视化呈现,这种表示方法依托于几何公理,以无刻度的直尺和圆规为工具,将抽象的代数运算转化为具体的几何构造,其原理严谨且操作清晰。
加法表示:线段拼接的几何实现
加法在尺规作图中的本质是“线段长度的叠加”,给定两个表示数值的线段,其和可通过将两线段在同一直线上首尾相接得到,具体步骤如下:
- 作基准线:用直尺作任意直线 ( l ),并在 ( l ) 上任取一点 ( A ) 作为起点。
- 截取第一线段:以圆规量取线段 ( a )(长度为数值 ( a )),将圆规针尖置于 ( A ),在 ( l )上截取点 ( B ),使得 ( AB = a )。
- 截取第二线段:保持圆规开口不变(或重新量取线段 ( b )),将针尖置于 ( B ),在 ( l )上同侧截取点 ( C ),使得 ( BC = b )。
- 得出和:线段 ( AC ) 的长度即为 ( a + b )。
关键原理:依据几何公理“两点之间线段最短”,且同一直上线段长度具有可加性,若 ( a = 3 ) cm,( b = 2 ) cm,则 ( AC = 5 ) cm,直观体现 ( 3 + 2 = 5 )。
特殊情况:若需表示多个数的加法(如 ( a + b + c )),可重复上述步骤,依次截取线段即可。
减法表示:线段截取的几何实现
减法是加法的逆运算,在尺规作图中体现为“从较长线段中截去较短线段,剩余部分即为差”,具体步骤如下:
- 作基准线:作直线 ( m ),取点 ( D ) 为起点。
- 截取被减数线段:量取线段 ( c )(长度为数值 ( c ),且 ( c > d )),将圆规针尖置于 ( D ),在 ( m )上截取点 ( E ),使得 ( DE = c )。
- 截取减数线段:量取线段 ( d )(长度为数值 ( d )),将圆规针尖置于 ( D ),在 ( DE ) 上截取点 ( F ),使得 ( DF = d )。
- 得出差:线段 ( FE ) 的长度即为 ( c - d )。
关键原理:线段长度具有非负性,且当 ( c > d ) 时,( FE = DE - DF = c - d ),若 ( c = 5 ) cm,( d = 2 ) cm,则 ( FE = 3 ) cm,对应 ( 5 - 2 = 3 )。
特殊情况:若需表示连续减法(如 ( c - d - e )),可在剩余线段上继续截取;若 ( c < d ),则需反向作图,以 ( d ) 为基准,截取 ( c ) 后剩余部分为 ( d - c )。
加减法的复合运算与几何验证
当问题涉及“( a + b - c )”或“( (a + b) - (c + d) )”等复合运算时,可通过分步操作实现,求 ( a + b - c )(假设 ( a + b > c )):
- 先作 ( AB = a ),延长 ( AB ) 至 ( C ),使 ( BC = b ),得 ( AC = a + b )。
- 在 ( AC ) 上截取 ( AD = c ),则 ( DC = AC - AD = a + b - c )。
几何验证:可通过三角形两边之和大于第三边等公理验证结果的合理性,若 ( a, b, c ) 为三角形三边,则 ( a + b > c ) 必然成立,( a + b - c ) 为正,与几何作图一致。
尺规作图与代数运算的对应关系
线段加减法与代数运算的对应关系可总结如下:
| 运算类型 | 代数表达式 | 尺规作图步骤 | 几何表示 |
|---|---|---|---|
| 加法 | ( a + b ) | 同一直线上首尾截取 ( a ) 和 ( b ) | 线段 ( AC = a + b ) |
| 减法 | ( c - d ) (( c > d )) | 截取 ( c ) 后,从同端截取 ( d ) | 线段 ( FE = c - d ) |
| 复合加法 | ( a + b + c ) | 依次截取三线段 | 线段 ( AD = a + b + c ) |
| 复合减法 | ( (a + b) - (c + d) ) | 先作和,再截减和 | 线段 ( GH = (a + b) - (c + d) ) |
实际应用与注意事项
尺规作图中的加减法不仅是基础技能,更是解决复杂几何问题(如线段分割、比例作图)的前提,在作黄金分割时,需通过线段减法确定关键点;在作多边形边长时,需通过加法累各边长度。
注意事项:
- 工具限制:仅能用无刻度直尺(不能测量长度)和圆规(不能量取角度),需严格遵循作图公理。
- 长度关系:减法中被减数长度必须大于减数,否则需通过反向作图或符号表示负值(古典尺规作图不涉及负值)。
- 精度问题:手工作图存在误差,理论上的精确性依赖于几何逻辑而非实际绘制。
相关问答FAQs
Q1:尺规作图能否表示负数的加减法?
A:古典尺规作图基于欧几里得几何,研究对象为长度、面积等非负量,因此无法直接表示负数,但若引入坐标系(如解析几何),可通过数轴的延伸方向表示正负,向右为正,向左为负”,减法可转化为反向加法。( 3 - 5 ) 可表示为从点 ( 3 ) 向左截取 ( 5 ) 个单位,得到点 ( -2 ),这已超出传统尺规作图的范畴。
Q2:如何用尺规作图验证 ( a + b > c ) 是否成立(三角形三边关系)?
A:可通过构造三角形验证,作线段 ( DE = a ),以 ( D ) 为圆心、( b ) 为半径画弧,以 ( E ) 为圆心、( c ) 为半径画弧,若两弧相交,则 ( a + b > c ) 成立(因为两弧相交意味着存在点 ( F ) 使得 ( DF = b )、( EF = c ),( DE + DF > EF )),若不相交,则 ( a + b \leq c ),无法构成三角形。