logit 命令用于逻辑回归，这是一种广泛使用的分类方法，特别是当你的因变量是二元（二值）变量时（是/否，成功/失败，购买/不购买）。

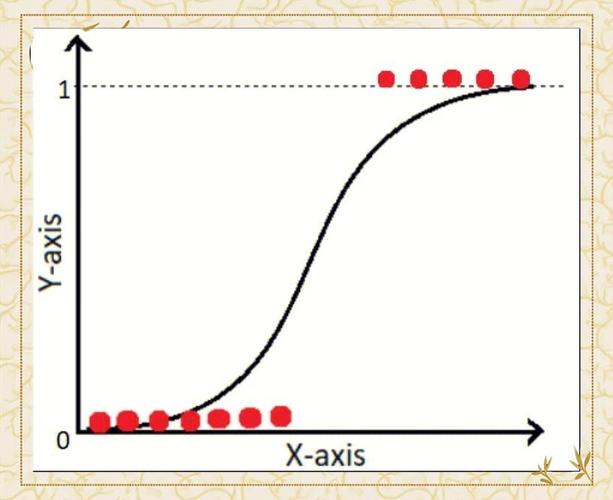
logit 是什么？为什么用它？

逻辑回归解决了线性回归无法处理二元因变量的问题，线性回归的预测值可能超出 [0, 1] 的范围，而概率必须在 [0, 1] 之间。

logit 模型通过Logit 转换，将一个事件的概率 p 转换为 log-odds（对数几率）,从而建立一个线性模型。

核心公式： log(p / (1-p)) = β₀ + β₁X₁ + β₂X₂ + ... + βₖXₖ

• p: 事件发生的概率 (e.g., P(Y=1))
• p / (1-p): Odds (几率),事件发生的概率与不发生的概率之比。
• log(p / (1-p)): Log-Odds (对数几率),这是因变量。
• β₀ + β₁X₁ + ...: 线性预测项,和我们熟悉的线性回归一样。

logit 与 probit 的区别： Stata 中另一个常用的二元回归命令是 probit,它们的主要区别在于链接函数：

• logit: 使用 Logit 链接函数，其误差项服从逻辑分布，系数的解释相对更直观（Odds Ratios）。
• probit: 使用 Probit 链接函数，其误差项服从标准正态分布。

在大多数应用场景下，两者的结果非常相似。logit 因其系数可以方便地转换为几率比，在社会科学、医学和流行病学等领域更受欢迎。

logit 命令的基本语法

logit depvar [indepvars] [if] [in] [, options]

参数详解：

• depvar: 因变量，必须是二元变量，取值通常为 0 和 1，Stata 会自动将 1 视为“成功”或“感兴趣的事件”。
• [indepvars]: 自变量（一个或多个），可以是连续变量（如年龄、收入）、分类变量（如性别、种族）或虚拟变量。
• [if] 和 [in]: 用于指定样本范围。if age > 18 只分析成年人；in 1/100 只分析前100个观测值。
• options: 可选参数,用于控制模型的输出和计算。

logit 的核心选项

a. 系数输出

• or: 最常用！ 在结果中直接显示几率比，而不是系数，这极大地简化了结果的解释。
  • 系数 表示自变量每增加一个单位，log-odds 的变化量。
  • 几率比 exp(β) 表示自变量每增加一个单位，几率 变为原来的多少倍，OR > 1，表示几率增加；OR < 1,表示几率减少。

b. 缺失值处理

• vce(robust): 使用稳健标准误，当数据存在异方差性时，这能提供更可靠的 p 值和置信区间,这是一个非常好的习惯。
• vce(cluster clustvar): 使用聚类稳健标准误，当数据存在组内相关性时（学生来自不同的学校）,这是必须的。

c. 模型拟合与诊断

• level(#): 设置置信区间的水平，默认为 95 (level(95))。
• noconstant: 模型中不包含常数项（截距），这非常罕见,通常不建议使用。

完整操作流程与实例

假设我们有一个数据集 auto.dta，我们想研究汽车的里程和是否为外国车如何影响其是否为高油耗车（mpg 高于某个值）。

步骤 1: 准备数据

// 加载数据
sysuse auto, clear
// 1. 创建二元因变量
// 我们定义 mpg 大于中位数为 "高油耗" (1)，否则为 "低油耗" (0)
summarize mpg
generate high_mpg = (mpg > r(mean))
label variable high_mpg "High Fuel Efficiency (1=High)"
tabulate high_mpg
// 2. 创建分类自变量 (foreign)
// foreign 是 0=国产, 1=进口，我们可以把它变成一个有标签的因子变量
// 虽然 logit 可以直接处理 0/1 变量，但作为因子变量有助于后续分析
// 这里我们直接使用，因为它是 0/1 变量
// 3. 检查自变量的多重共线性（可选但推荐）
// 对于连续变量，可以计算 VIF
// 注意：logit 后不能直接用 `vif`，需要先跑 `regress` 估计
regress mpg weight foreign
estat vif // VIF > 10 可能存在严重多重共线性

步骤 2: 运行 logit 模型

模型 1: 基础模型 我们想看 weight（车重）和 foreign（是否进口）对 high_mpg 的影响。

// 运行 logit 模型，输出系数 (log-odds)
logit high_mpg weight foreign
// 输出结果解读：
// weight 的系数为负，表示车重越大，成为高油耗车的 log-odds 越低。
// foreign 的系数为正，表示进口车成为高油耗车的 log-odds 更高。

模型 2: 带几率比 的模型 (更常用)

// 运行 logit 模型，并直接输出几率比
logit high_mpg weight foreign, or
// 输出结果解读：
// 1. weight: OR = exp(-0.00395) ≈ 0.996
//    解释：车重每增加1磅，汽车是高油耗车的**几率**会变为原来的 0.996 倍。
//    换句话说，车重越大，是高油耗车的几率越低。
// 2. foreign: OR = exp(2.246) ≈ 9.45
//    解释：相比于国产车，进口车是高油耗车的**几率**是国产车的 9.45 倍。
//    这说明进口车更有可能是高油耗车（在我们的定义下，即 mpg 高）。

模型 3: 使用稳健标准误

// 使用稳健标准误重新运行模型
logit high_mpg weight foreign, or vce(robust)
// 比较前后两模型的系数和标准误，如果变化不大，说明异方差问题不严重。
// 如果标准误变化很大，则必须使用稳健标准误。

结果解读

logit 的输出表主要关注以下几点：

当你使用 , or 选项后，整个表格会变成几率比：

几率比 的解读黄金法则：

• OR = 1: 该变量对事件发生的几率没有影响。
• OR > 1: 该变量会增加事件发生的几率，OR=2.5 表示“几率变为原来的2.5倍”。
• OR < 1: 该变量会减少事件发生的几率，OR=0.8 表示“几率变为原来的0.8倍”。

后续分析与预测

模型跑完后,你通常还需要做一些后续分析。

a. 预测概率

这是将 log-odds 转换回概率的最直观方式。

// 1. 运行模型
logit high_mpg weight foreign, or
// 2. 预测概率
// 生成一个新变量存储预测概率
predict pr_hat
// 查看预测概率的分布
summarize pr_hat
// 可以将预测概率与实际值进行对比
// 找出模型预测为高概率但实际不是的样本
gen predicted_high = (pr_hat > 0.5) // 以0.5为阈值
tab predicted_high high_mpg, row

b. 计算边际效应

logit 模型中的系数是常数，但边际效应（即自变量变化一个单位对概率的影响）却不是，它会随着所有自变量的取值而变化，计算边际效应通常在某个“代表性”的样本点上（如均值或所有观测值）进行。

// 方法1: 使用 `margins` 命令 (推荐，更灵活)
// 计算所有自变量在均值处的边际效应
margins, dydx(*) atmeans
// 计算所有自变量对所有观测值的平均边际效应
margins, dydx(*)
// 方法2: 使用 `mfx` 命令 (较老的方法)
mfx compute, predict(p)

c. 模型拟合优度

• Pseudo R²: logit 没有真正的 R²，但有一个“伪R²”，它类似于线性回归中的R²，表示模型相比只有截距的模型（空模型）在解释因变量变异方面的改进程度。McFadden's Pseudo R² 是最常见的，其值在0到1之间，但通常远小于线性回归的R²，0.2-0.4可能就算是一个不错的模型了。

• ROC曲线 & AUC值: 用于评估模型的分类能力。

  // 首先需要安装 `roc` 命令 (如果未安装)
  // ssc install roctab
  // 使用预测概率和实际值绘制ROC曲线
  roc pr_hat high_mpg
  // 计算AUC值 (Area Under the Curve)
  // AUC > 0.7 表示有一定区分能力，> 0.8 表示区分能力较好。

常见问题与注意事项

1. 样本量: logit 是一个最大似然估计方法，需要足够的样本量，一个经验法则是，每个自变量至少需要 10-20 个“成功”事件和 10-20 个“失败”事件。
2. 完全分离或准完全分离: 如果某个自变量或自变量的组合可以完美地预测因变量（所有年龄>60的人都成功，而所有年龄<60的人都失败），模型的系数会变得无穷大，Stata 会给出警告，这时需要考虑使用 probit、Firth's penalized logistic regression (firthlogit) 或移除问题变量。
3. 变量转换: 和线性回归一样，检查自变量与 log-odds 之间是否存在线性关系，如果不是，可能需要对自变量进行转换（如取对数、多项式项）。
4. 分类变量的处理: 如果分类自变量有多个水平（如 region 有 东部、中部、西部），需要将其转换为虚拟变量（dummy variables），Stata 的因子变量标记法（如 i.region）可以轻松实现。

   // 假设 region 是 1,2,3...
   logit high_mpg weight i.foreign i.region, or

希望这份详细的指南能帮助你掌握 Stata 的 logit 命令！