除法如何表示成连减,是数学中一种基础且直观的运算转换方法,它揭示了除法与减法之间的内在联系,从本质上讲,除法表示的是“一个数(被除数)包含多少个另一个数(除数)”,而连减则通过重复减去除数,直到被除数不再足够减去除数,从而得到商和余数,这种表示方法不仅有助于理解除法的本质,也为后续学习更复杂的数学概念奠定了基础。
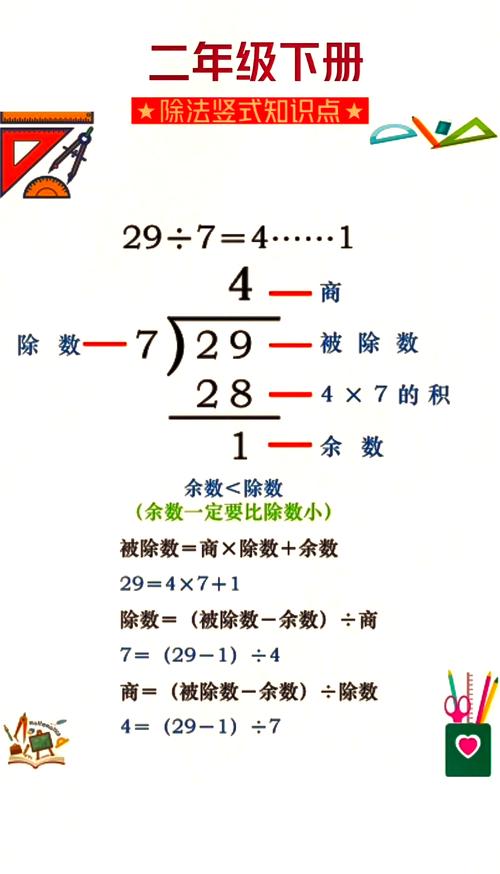
要理解除法如何表示成连减,我们首先需要明确除法的基本要素,在除法算式“a ÷ b = c……d”中,a 是被除数,b 是除数,c 是商,d 是余数,且余数 d 必须满足 0 ≤ d < b,将除法转化为连减,就是不断地从被除数 a 中减去除数 b,记录减法的次数,直到剩下的数(即余数)小于除数 b,减法的次数就是商 c,剩下的数就是余数 d。
计算 15 ÷ 3,我们可以进行如下连减:15 - 3 = 12,12 - 3 = 9,9 - 3 = 6,6 - 3 = 3,3 - 3 = 0,我们总共减了 5 次 3,才得到 0,15 ÷ 3 = 5,余数为 0,再比如计算 17 ÷ 5,连减过程为:17 - 5 = 12,12 - 5 = 7,7 - 5 = 2,此时剩下的 2 已经小于除数 5,无法再继续减下去,所以我们减了 3 次 5,得到商为 3,余数为 2,即 17 ÷ 5 = 3……2。
为了更清晰地展示这种转换关系,我们可以通过表格来对比除法算式与对应的连减过程,以下是一个简单的示例表格:
| 除法算式 | 被除数 (a) | 除数 (b) | 连减过程 | 减法次数 (商 c) | 余数 (d) | 结果 (a ÷ b = c……d) |
|---|---|---|---|---|---|---|
| 15 ÷ 3 | 15 | 3 | 15 - 3 = 12;12 - 3 = 9;9 - 3 = 6;6 - 3 = 3;3 - 3 = 0 | 5 | 0 | 15 ÷ 3 = 5……0 |
| 17 ÷ 5 | 17 | 5 | 17 - 5 = 12;12 - 5 = 7;7 - 5 = 2 | 3 | 2 | 17 ÷ 5 = 3……2 |
| 20 ÷ 6 | 20 | 6 | 20 - 6 = 14;14 - 6 = 8;8 - 6 = 2 | 3 | 2 | 20 ÷ 6 = 3……2 |
| 10 ÷ 2 | 10 | 2 | 10 - 2 = 8;8 - 2 = 6;6 - 2 = 4;4 - 2 = 2;2 - 2 = 0 | 5 | 0 | 10 ÷ 2 = 5……0 |
| 8 ÷ 4 | 8 | 4 | 8 - 4 = 4;4 - 4 = 0 | 2 | 0 | 8 ÷ 4 = 2……0 |
从表格中可以明显看出,连减的次数与除法中的商完全一致,而连减最后剩下的数就是余数,这种方法在处理较小的整数除法时尤为直观,能够帮助我们快速理解除法的“包含”意义,20 ÷ 6 表示 20 中包含多少个 6,通过连减 6 三次后剩下 2,说明 20 包含 3 个 6,还多出 2,因此商是 3,余数是 2。

除法表示成连减的方法不仅适用于整数除法,在特定条件下也可以推广到小数除法,但其过程会更为复杂,因为需要处理小数点后的位数,计算 1 ÷ 0.2,我们可以将被除数和除数同时乘以 10,转化为 10 ÷ 2,然后进行连减:10 - 2 = 8;8 - 2 = 6;6 - 2 = 4;4 - 2 = 2;2 - 2 = 0,共减了 5 次,1 ÷ 0.2 = 5,这种转化利用了除法的基本性质,即被除数和除数同时扩大或缩小相同的倍数,商不变,从而将小数除法转化为整数除法,再用连减法求解。
在实际应用中,连减法虽然直观,但对于较大的数字或复杂的除法运算,其效率远低于传统的竖式除法,竖式除法通过抽象和符号化的运算,大大简化了计算过程,连减法作为理解除法本质的重要工具,在数学教育中具有不可替代的作用,它能够帮助初学者,特别是小学生,建立对除法的直观认识,理解商和余数的实际意义,在分配物品时,如果有 17 个苹果,每个小朋友分 5 个,用连减法可以清楚地看到,可以分给 3 个小朋友(5 + 5 + 5 = 15),还剩下 2 个苹果无法再完整分给一个小朋友,这 3 就是商,2 就是余数。
除法表示成连减也为后续学习更高级的数学概念提供了基础,在研究数论中的整除性、最大公约数和最小公倍数等问题时,反复运用减法(或其变种——辗转相除法)是一种常见的解题思路,辗转相除法正是基于“较大的数减去较小的数”这一原理,通过连续的减法(或更高效的除法)来求两个数的最大公约数,这可以看作是连减法在数学中的延伸和应用。
需要注意的是,在使用连减法表示除法时,必须确保每次减去的都是除数本身,并且减法过程要持续进行,直到余数小于除数,如果中途停止或减去的数不是除数,就会得到错误的结果,在计算 17 ÷ 5 时,如果只减两次 5(17 - 5 - 5 = 7),就停止运算,那么会错误地认为商是 2,余数是 7,而实际上余数 7 仍然大于除数 5,说明还可以继续减去除数,余数必须小于除数是判断连减过程是否完成的关键条件。
除法表示成连减是一种将抽象的除法运算转化为具体、重复的减法过程的方法,它通过不断地从被除数中减去除数,直到剩余数小于除数,从而得到商和余数,这种方法不仅揭示了除法的“包含”本质,也为理解商和余数的概念提供了直观的途径,虽然在处理大数时效率不高,但其在数学教育和基础概念理解方面具有重要的价值,是连接减法与除法这两种基本运算的重要桥梁,通过掌握这种方法,我们可以更深刻地理解数学运算之间的内在联系,为进一步学习数学知识打下坚实的基础。
相关问答 FAQs
问题 1:为什么除法可以表示成连减?这种表示方法有什么意义?
解答:除法可以表示成连减,是因为除法的本质是求一个数(被除数)中包含多少个另一个数(除数),连减的过程就是不断地从被除数中去除除数,每减一次,就相当于“包含”了一个除数,直到剩余的数不足以再减去除数为止,减法的次数就是商,剩余的数就是余数,这种表示方法的意义在于它将抽象的除法运算转化为具体、直观的减法过程,有助于初学者理解除法的本质含义,特别是商和余数的实际意义,它揭示了除法与减法之间的内在联系,是数学中不同运算相互转化、相互依存的具体体现,为后续学习更复杂的数学概念(如辗转相除法)奠定了基础。
问题 2:在使用连减法将除法转化为连减时,如何判断运算是否可以停止?余数有什么要求?
解答:在使用连减法将除法转化为连减时,运算停止的关键条件是:余数必须小于除数,就是不断地从被除数中减去除数,每次减去一个完整的除数,并记录减法的次数,当某一次减法后,剩下的数(即当前的余数)已经小于除数时,就无法再进行完整的减法操作了,此时连减过程结束,记录的减法总次数就是商,最后剩下的那个小于除数的数就是余数,计算 15 ÷ 4,连减过程为:15 - 4 = 11,11 - 4 = 7,7 - 4 = 3,此时剩下的 3 小于除数 4,运算停止,共减了 3 次,所以商是 3,余数是 3,如果余数大于或等于除数,说明还可以继续减去除数,运算尚未完成,余数必须满足 0 ≤ 余数 < 除数这一条件,这是判断连减过程是否正确完成的重要标准。