计算混合图形的面积是几何学中常见的问题,混合图形通常由基本几何图形(如三角形、矩形、圆形、梯形等)组合或拼接而成,其核心思路是将复杂图形分解为若干个简单图形,分别计算每个简单图形的面积,最后将各部分面积相加(或相减,若存在重叠或空洞部分),以下是详细的计算步骤、方法及示例说明。
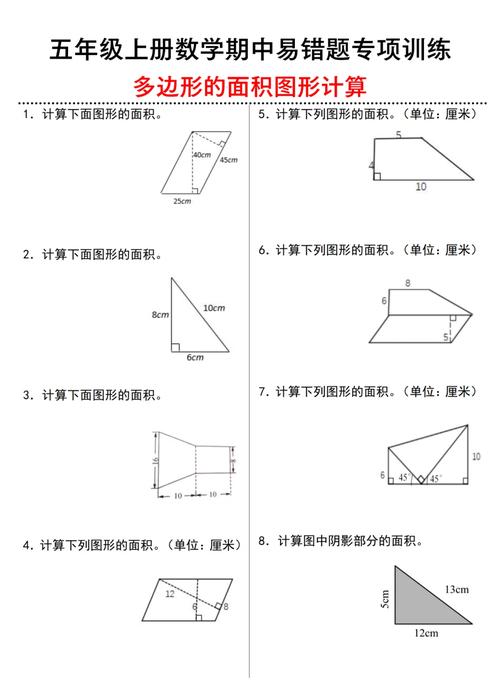
分解混合图形
首先需要观察混合图形的结构,通过辅助线(如分割线、延长线等)将其拆分为若干个基本图形,分解时应遵循以下原则:
- 完整性:分解后的图形必须覆盖整个混合图形,无遗漏或重叠(除非重叠部分需单独处理)。
- 简便性:选择最少的分割方式,使每个子图形均为易于计算的基本图形(如三角形、矩形等)。
- 标注清晰:在图形上标注必要的数据(如边长、半径、角度等),避免遗漏关键信息。
一个由半圆和直角三角形组成的混合图形,可通过半圆的直径作为分割线,将其分解为半圆和直角三角形两部分。
计算各子图形的面积
根据分解后的基本图形类型,选择对应的面积公式进行计算,常见基本图形的面积公式如下表所示:
| 图形类型 | 面积公式 | 参数说明 |
|---|---|---|
| 矩形 | ( S = a \times b ) | ( a )、( b ) 为长和宽 |
| 三角形 | ( S = \frac{1}{2} \times \text{底} \times \text{高} ) | 底与高对应 |
| 梯形 | ( S = \frac{1}{2} \times (a + b) \times h ) | ( a )、( b ) 为上底和下底,( h ) 为高 |
| 圆形 | ( S = \pi r^2 ) | ( r ) 为半径 |
| 扇形 | ( S = \frac{n}{360} \times \pi r^2 ) | ( n ) 为圆心角度数 |
| 半圆 | ( S = \frac{1}{2} \pi r^2 ) | ( r ) 为半径 |
示例1:计算一个由矩形和半圆组成的混合图形(如下图),已知矩形长为10 cm,宽为5 cm,半圆直径与矩形宽重合。
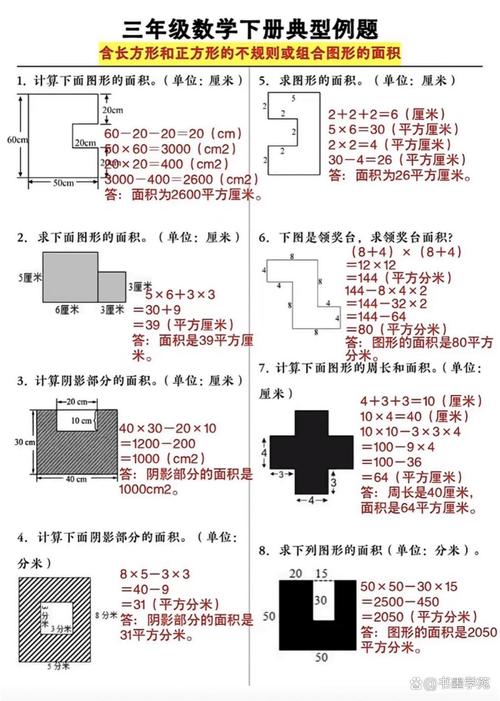
- 分解:矩形 + 半圆。
- 矩形面积:( S_1 = 10 \times 5 = 50 \, \text{cm}^2 )。
- 半圆半径:( r = \frac{5}{2} = 2.5 \, \text{cm} ),面积:( S_2 = \frac{1}{2} \pi (2.5)^2 \approx 9.82 \, \text{cm}^2 )。
- 总面积:( S = S_1 + S_2 = 50 + 9.82 = 59.82 \, \text{cm}^2 )。
处理重叠或空洞部分
若混合图形中存在重叠区域或空洞,需采用“加法”或“减法”原则:
- 重叠部分:若两个图形有重叠,总面积 = 图形A面积 + 图形B面积 - 重叠部分面积。
- 空洞部分:若图形内部有空洞(如矩形内部挖去一个圆形),总面积 = 外部图形面积 - 空洞面积。
示例2:一个边长为8 cm的正方形内部有一个内切圆,计算剩余部分的面积。
- 正方形面积:( S_1 = 8 \times 8 = 64 \, \text{cm}^2 )。
- 内切圆半径:( r = \frac{8}{2} = 4 \, \text{cm} ),面积:( S_2 = \pi \times 4^2 \approx 50.27 \, \text{cm}^2 )。
- 剩余面积:( S = S_1 - S_2 = 64 - 50.27 = 13.73 \, \text{cm}^2 )。
使用坐标法计算不规则混合图形
对于无法直接分解的复杂混合图形,可采用坐标法(如鞋带公式)计算面积,步骤如下:
- 确定图形顶点的坐标(按顺时针或逆时针顺序排列)。
- 代入鞋带公式:
[ S = \frac{1}{2} \left| \sum_{i=1}^{n} (xi y{i+1} - x_{i+1} yi) \right| \quad (\text{ \, x{n+1} = x1, y{n+1} = y_1) ]
示例3:一个四边形顶点坐标为 ( A(0,0) )、( B(3,0) )、( C(4,2) )、( D(1,3) ),计算其面积。
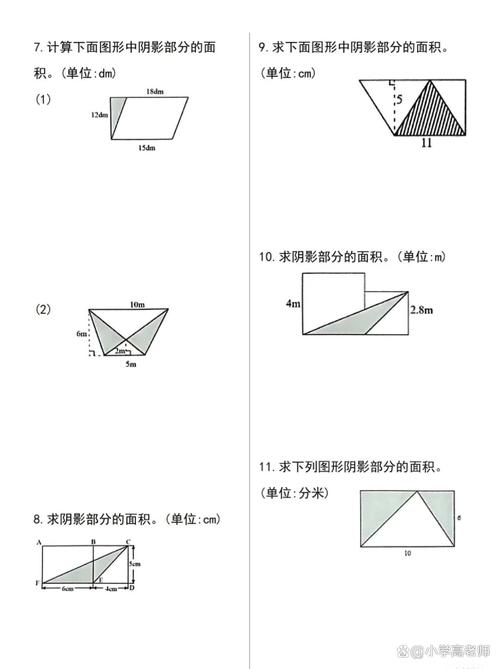
- 代入公式:
[ S = \frac{1}{2} \left| (0 \times 0 + 3 \times 2 + 4 \times 3 + 1 \times 0) - (0 \times 3 + 0 \times 4 + 2 \times 1 + 3 \times 0) \right| = \frac{1}{2} \left| (0 + 6 + 12 + 0) - (0 + 0 + 2 + 0) \right| = \frac{1}{2} \times 16 = 8 ] - 面积为8平方单位。
注意事项
- 单位统一:确保所有长度的单位一致,避免单位混淆导致错误。
- 图形顺序:使用鞋带公式时,顶点顺序必须为顺时针或逆时针,不可交叉排列。
- 近似值处理:若结果含π,可根据题目要求保留π或取近似值(如3.14)。
相关问答FAQs
问题1:如果混合图形中包含多个圆形或扇形,如何快速计算总面积?
解答:将所有圆形或扇形的面积分别计算后相加,若存在重叠,需减去重叠部分的面积,两个半径为3 cm的圆相交,重叠部分为半径为3 cm的60°扇形,则总面积 = ( 2 \times \pi \times 3^2 - \frac{60}{360} \times \pi \times 3^2 = 18\pi - 1.5\pi = 16.5\pi \, \text{cm}^2 )。
问题2:如何验证混合图形面积计算结果的正确性?
解答:可通过分割方式验证(如用不同辅助线分解图形,结果应一致)或估算法(如将图形近似为规则图形,估算面积范围是否合理),利用CAD软件或几何画板工具绘制图形并直接测量面积也是一种有效验证手段。




