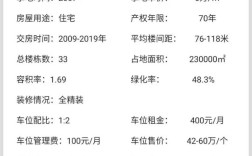
向量是数学中描述既有大小又有方向的量,而实数则是仅表示大小的标量,两者之间的联系是线性代数和几何学的基础,主要通过数乘运算、线性组合、内积等核心概念建立,这种联系不仅赋予向量更丰富的运算性质,也为解决实际问题提供了工具。

数乘运算是向量与实数最直接的联系方式,给定一个向量v=(v₁, v₂, ..., vₙ)和一个实数k,数乘kv定义为将向量的每个分量都乘以k,即kv=(kv₁, kv₂, ..., kvₙ),几何上,数乘实现了对向量的“伸缩”或“反向”:当k>1时,向量沿原方向伸长;0<k<1时缩短;k=0时退化为零向量;k<0时方向反转,若v表示位移“向东3米”,则2v表示“向东6米”,-0.5v表示“向西1.5米”,数乘满足结合律、分配律等运算律,确保了向量空间对线性运算的封闭性。
向量的线性组合进一步深化了与实数的联系,有限个向量v₁, v₂, ..., vₘ的线性组合是指形如k₁v₁+k₂v₂+...+kₘvₘ的表达式,其中k₁, k₂, ..., kₘ均为实数,线性组合是向量空间的核心概念:向量空间的基就是一组线性无关的向量,空间中任意向量都可唯一表示为基向量的线性组合,系数即为该向量在此基下的坐标,在二维平面中,标准基i=(1,0)、j=(0,1)的线性组合ai+bj=(a,b)可表示任意平面向量,实数a、b直接对应向量的横纵坐标。
内积(点积)是向量与实数联系的另一种重要形式,两个n维向量u=(u₁, u₂, ..., uₙ)与v=(v₁, v₂, ..., vₙ)的内积定义为u·v=u₁v₁+u₂v₂+...+uₙvₙ,结果是一个实数,内积的几何意义是u的模与v在u上投影的乘积,即u·v=|u||v|cosθ(θ为夹角),通过内积,可衍生出向量的模(长度)|v|=√(v·v)、向量的正交性(u·v=0时垂直)等几何性质,在物理中,力F与位移s的内积F·s表示功(实数),直接体现了向量运算与实际标量的联系。
实数还通过标量场与向量场建立间接联系,温度场中每点的温度是实数(标量场),而温度梯度(指向温度升高最快的方向)是向量场,梯度向量的模(实数)表示温度变化率,这种联系在多元微积分和物理学中极为重要。
以下表格总结了向量与实数的主要联系方式:
| 联系方式 | 定义/形式 | 几何/物理意义 | 应用举例 |
|---|---|---|---|
| 数乘运算 | kv=(kv₁, kv₂, ..., kvₙ) | 向量伸缩(k>0伸长,k<0反向缩短) | 调整速度大小、力的合成 |
| 线性组合 | k₁v₁+k₂v₂+...+kₘvₘ | 向量分解与合成,坐标表示 | 基底下的坐标表示、向量空间生成 |
| 内积(点积) | u·v=u₁v₁+...+uₙvₙ | 投影关系、夹角计算、功的计算 | 判断垂直、计算功、向量投影 |
| 模(长度) | |v|=√(v·v) | 向量的欧几里得长度 | 距离计算、向量标准化 |
相关问答FAQs:
Q1:实数与向量的数乘运算和向量间的加法运算有何共同作用?
A1:数乘与向量加法共同构成了线性运算的基础,满足封闭性(运算结果仍为向量)、结合律、交换律(加法)和分配律(数乘对加法),这两种运算使得向量集合构成线性空间(向量空间),允许对向量进行分解、合成和坐标表示,是线性代数研究向量结构的核心工具。
Q2:为什么内积的结果是实数,它如何反映向量的几何关系?
A2:内积定义为对应分量乘积之和,分量均为实数,故结果为实数,几何上,内积u·v=|u||v|cosθ通过实数结果隐含了向量间的夹角θ(cosθ=u·v/(|u||v|))和投影关系(|v|cosθ为v在u上的投影长度),当内积为零时,cosθ=0,表明两向量垂直;内积的正负则反映夹角是否为锐角或钝角,从而将代数运算与几何性质紧密联系。