在MATLAB中，逆矩阵的计算是线性代数操作中的常见需求，逆矩阵即对于一个方阵A，若存在另一个方阵B，使得AB=BA=I（I为单位矩阵），则B称为A的逆矩阵，记作A⁻¹，MATLAB提供了多种计算逆矩阵的方法，其中最常用的是inv函数，此外还有基于矩阵分解的间接计算方式，这些方法在不同场景下各有优势,以下将详细介绍MATLAB中逆矩阵的相关命令及其使用注意事项。
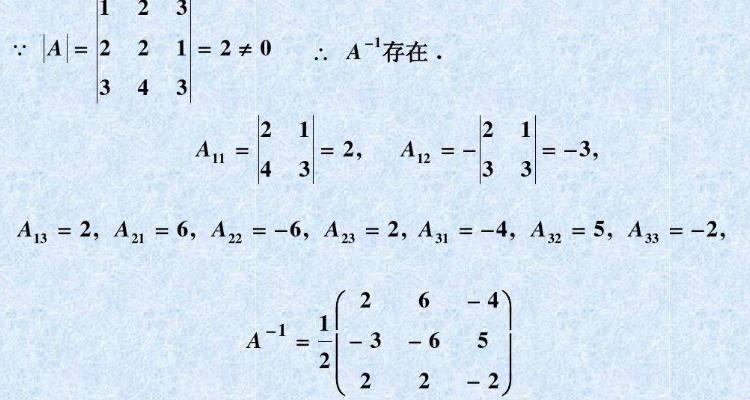
核心命令：inv函数
inv是MATLAB中计算逆矩阵最直接的函数，其语法为Y = inv(X)，其中X必须是方阵，且行列式不为零（即可逆矩阵）,若定义一个3阶方阵A：
A = [1 2 3; 0 1 4; 5 6 0];
通过inv_A = inv(A)即可得到其逆矩阵，计算结果可以通过A * inv_A验证，理论上应接近单位矩阵（由于浮点数精度误差，结果可能存在微小偏差），需要注意的是，inv函数在处理病态矩阵（接近奇异矩阵）时可能产生较大误差，此时建议使用条件数函数cond(A)检查矩阵的可逆性，条件数越大，矩阵越接近奇异,逆矩阵计算误差越大。
基于矩阵分解的逆矩阵计算
除了直接使用inv，MATLAB还可通过矩阵分解方法计算逆矩阵，这种方式在数值稳定性上更具优势，尤其适用于大型矩阵或病态矩阵，常见的分解方法包括LU分解、Cholesky分解等。
-
LU分解法
通过lu函数将矩阵A分解为下三角矩阵L和上三角矩阵U的乘积（A=LU）,则逆矩阵可通过求解线性方程组得到。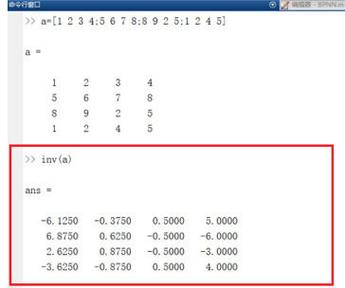
（图片来源网络，侵删）[L, U] = lu(A); inv_A = U \ (L \ eye(size(A)));
这种方法避免了直接计算逆矩阵可能带来的数值误差,适合大型稀疏矩阵。
-
Cholesky分解法
若矩阵A为对称正定矩阵，可使用chol函数进行Cholesky分解（A=RᵀR），其中R为上三角矩阵,逆矩阵计算为：R = chol(A); inv_A = R \ (R' \ eye(size(A)));
Cholesky分解在处理正定矩阵时效率更高,且数值稳定性较好。
逆矩阵计算的性能与适用场景
不同方法的计算效率和适用场景存在差异,可通过下表对比：
| 方法 | 适用矩阵类型 | 数值稳定性 | 计算效率 | 推荐场景 |
|---|---|---|---|---|
inv(A) |
一般方阵 | 中等 | 高（小矩阵） | 小型稠密矩阵的快速计算 |
| LU分解法 | 一般方阵 | 高 | 中等 | 大型矩阵或病态矩阵 |
| Cholesky分解法 | 对称正定矩阵 | 高 | 高 | 对称正定矩阵的高效计算 |
注意事项
- 矩阵可逆性检查：计算逆矩阵前需确认矩阵可逆，可通过
det(A)（行列式不为零）或rank(A)（满秩）初步判断，但更可靠的方法是计算条件数cond(A)，当条件数过大时（如>1e10），矩阵可能接近奇异,逆矩阵结果不可信。 - 浮点数精度问题：MATLAB采用双精度浮点数计算，逆矩阵结果可能存在微小误差，验证时可通过
norm(A*inv_A - eye(size(A)))计算误差范数。 - 稀疏矩阵处理：对于大型稀疏矩阵，建议使用稀疏矩阵存储格式（如
sparse(A)）并结合分解法计算,以提高内存和计算效率。
相关问答FAQs
问题1：MATLAB中如何判断矩阵是否可逆？
解答：判断矩阵可逆可通过以下方法：（1）计算行列式det(A)，若结果不为零则矩阵可逆，但行列式对数值误差敏感，不适用于大型矩阵；（2）计算矩阵的秩rank(A)，若秩等于矩阵阶数，则矩阵满秩可逆；（3）计算条件数cond(A)，条件数越小，矩阵可逆性越好，通常认为条件数大于1e10时矩阵接近奇异，逆矩阵不可用，综合而言，cond(A)是最可靠的判断方法。
问题2：为什么大型矩阵不建议直接使用inv函数计算逆矩阵？
解答：大型矩阵直接使用inv函数存在两个主要问题：（1）数值稳定性差：inv函数基于高斯消元法，对病态矩阵的数值误差放大效应明显，而分解法（如LU分解）通过分步求解能更好控制误差；（2）计算效率低：inv函数会显式计算逆矩阵并存储，而实际应用中往往只需解线性方程组Ax=b，此时使用A\b（即矩阵左除）可直接得到解，无需显式计算逆矩阵，且A\b会根据矩阵特性自动选择最优算法（如分解法），效率更高，大型矩阵推荐使用分解法或矩阵左除代替inv。
