除法竖式的有效教学需要遵循学生的认知规律,从具体到抽象,逐步引导理解算理、掌握算法,教学中应注重情境创设、操作体验、算理可视化,并通过分层练习巩固技能,同时关注易错点的针对性指导。

情境导入是激发兴趣的关键,教师可创设与学生生活密切相关的情境,如“分糖果”“整理图书”等,让学生在解决实际问题中感受除法的意义,给出“把48颗糖果平均分给4个小朋友,每人分几颗?”的问题,引导学生列出算式48÷4,自然过渡到竖式计算,情境导入要避免脱离实际,让学生体会到数学与生活的联系,增强学习内驱力。
通过操作活动理解算理,除法竖式的核心是“分的过程”,需借助小棒、计数器等学具帮助学生直观理解,例如教学48÷4时,可让学生先用小棒操作:先分4捆(每捆10根)给4个小朋友,每人1捆(10根),再分8根单根,每人2根,合起来每人12根,操作后引导学生思考:竖式中的“4”写在十位上表示什么?“8”是怎么来的?每一步计算对应操作中的哪个环节?通过学具与算式的对应,将抽象的竖式步骤转化为具体的分物过程,帮助学生理解“先分十位,再分个位”的顺序和“商的对位”原理。
利用可视化工具拆解竖式结构,除法竖式包含被除数、除数、商、余数等要素,教学时需用彩色粉笔或课件标注各部分名称及计算流程,以48÷4为例,分步拆解:① 先看被除数最高位“4”(十位),4÷4=1,商1写在十位上,表示1个十;② 1×4=4,写在4的下面,4-4=0,表示十位分完没有剩余;③ 将个位8落下来,8÷4=2,商2写在个位上,表示2个一;④ 2×4=8,8-8=0,计算结束,通过流程图或表格对比每一步的操作(如表1),帮助学生清晰掌握竖式书写的规范步骤。
表1:48÷4竖式步骤解析
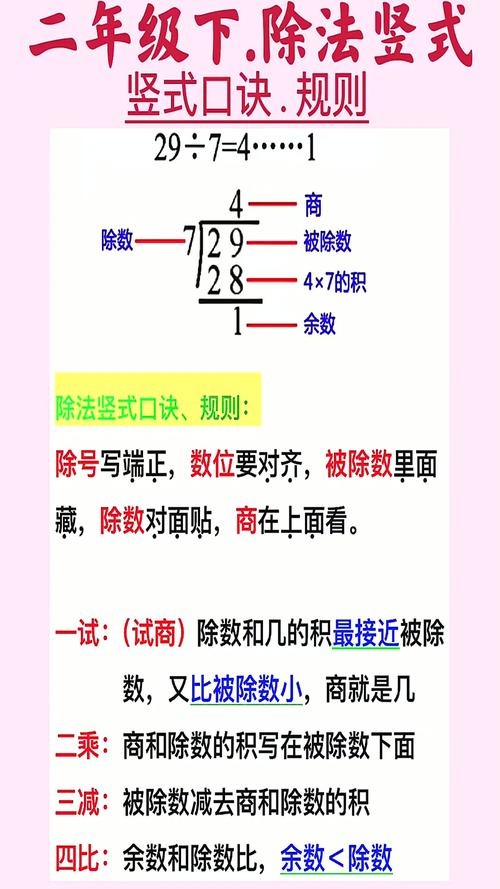
| 计算步骤 | 竖式书写 | 对应操作 | 算理说明 |
|---|---|---|---|
| 分十位 | 4 ) 4 8 | 先分4捆小棒 | 4个十÷4=1个十,商1对十位 |
| 减十位 | - 4 | 1×4=4,减去4个十 | 十位分完余0 |
| 落个位 | 0 8 | 落下8根单根 | 个位8参与运算 |
| 分个位 | - 8 | 再分8根单棒 | 8个一÷4=2个一,商2对个位 |
| 结束 | 0 | 2×4=8,减去8 | 个位分完无余数 |
在学生理解算理后,需强调竖式书写的规范性:数位对齐、从高位算起、余数必须小于除数等,可通过对比错例(如商的数位写错、余数大于除数)加深印象,例如展示“48÷4=2”的错误竖式,引导学生讨论错因,强化“商的位数要与被除数位数对应”的意识。
分层练习是巩固技能的重要环节,设计基础题(如两位数除以一位数,无余数)、变式题(如商中间有0、有余数)、拓展题(如三位数除以一位数),满足不同学生需求,基础题要求规范书写,变式题重点突破“0占位”和“余数处理”,拓展题则引导迁移算理,例如练习“306÷3”时,强调“十位0不够除,商0占位”,避免漏写。
针对易错点,可采用“错题医院”活动,收集典型错例(如余数未小于除数、商的数位对齐错误),让学生当“小医生”诊断病因,集体订正,例如针对“62÷3=20……2”的错误(商应为20余2,学生易写成21),通过摆小棒演示:6捆小棒分3份,每份2捆(20根),剩下2根不够分,明确“余数必须小于除数”的规则。
总结反思促进知识内化,引导学生回顾“分物操作—竖式步骤—算理理解”的过程,用自己的语言描述除法竖式的计算方法,例如提问:“竖式中的每一步实际在分什么?”“为什么商要对着数位写?”通过总结,帮助学生构建完整的知识体系。

相关问答FAQs:
问:学生经常出现商的数位写错(如把48÷4的商写成21),如何纠正?
答:可借助计数器演示:先在十位拨4颗珠子,分4份得1个十,商1对十位;再在个位拨8颗珠子,分4份得2个一,商2对个位,通过“数位与珠子的一一对应”,强化“商的数位要对齐”的意识,并对比错误写法(如商21表示2个十和1个一,实际应为1个十和2个一),让学生直观感受数位错位的后果。
问:如何让学生理解“余数必须小于除数”?
答:用生活实例解释:如“17个苹果分给3人,每人5个,余2个(17÷3=5……2)”;若商6,则需6×3=18个苹果,比17个还多,不够分,再通过摆小棒操作:17根小棒分3份,每份5根(15根),剩下2根不够再分1份,明确“余数是剩下的不够再分的部分,必须比除数小”,可设计“余数游戏”:给定除数,让学生摆出不同的余数,找出“余数必须小于除数”的规律,加深理解。


