在几何学中,弧的中位线是一个重要的概念,它指的是连接弧的两个端点与弧的中点所形成的线段,理解如何求弧的中位线不仅有助于解决几何问题,还能为后续学习更复杂的曲线性质打下基础,本文将详细探讨弧的中位线的定义、求解方法及其应用,并结合实例说明具体步骤。
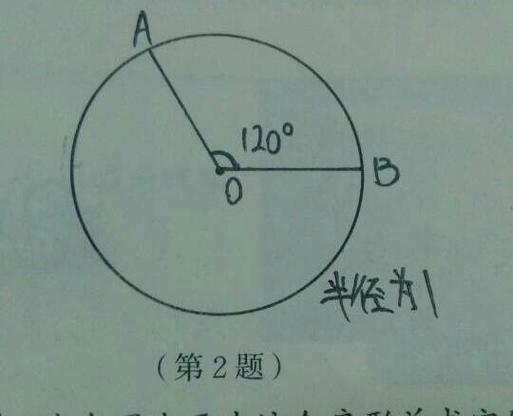
我们需要明确弧的中位线的定义,弧是圆周的一部分,由圆上的两点和这两点之间的圆周组成,弧的中点是指将弧的长度平分的点,即从弧的一个端点到中点的弧长等于从中点到另一个端点的弧长,弧的中位线则是连接弧的两个端点与弧的中点所形成的线段,值得注意的是,弧的中位线与弦的中位线不同,弦的中位线是连接弦的两个端点与弦的中点的线段,而弧的中位线涉及的是弧的几何性质。
我们探讨如何求弧的中位线,假设有一个圆,其圆心为O,半径为r,弧的两个端点为A和B,弧的中点为M,我们的目标是找到线段AM和BM的长度,即弧的中位线长度,以下是详细的求解步骤:
-
确定弧的圆心角:首先需要计算弧AB所对应的圆心角θ,圆心角是指圆心O与弧的两个端点A、B形成的夹角,如果已知弧的长度l,可以通过公式θ = l / r(θ以弧度制表示)求出圆心角,如果已知弧的度数,可以直接使用该度数作为圆心角。
-
计算弧的中点M的位置:弧的中点M位于弧AB的平分线上,即圆心角∠AOM = ∠BOM = θ/2,这意味着从OA到OM的角度为θ/2,从OB到OM的角度也为θ/2,可以通过旋转或几何作图找到点M的位置。
 (图片来源网络,侵删)
(图片来源网络,侵删) -
计算中位线AM和BM的长度:由于AM和BM是圆的两条弦,我们可以利用弦长公式来计算它们的长度,弦长公式为:弦长 = 2r sin(α/2),是弦所对应的圆心角,对于AM,对应的圆心角是θ/2,因此AM = 2r sin(θ/4),同理,BM = 2r sin(θ/4),由于M是弧的中点,AM和BM的长度相等,因此弧的中位线长度为2r sin(θ/4)。
为了更直观地理解这一过程,我们可以通过一个具体的例子来说明,假设有一个圆,半径r = 5,弧AB的长度为10π/3,首先计算圆心角θ:θ = l / r = (10π/3) / 5 = 2π/3(即120度),弧的中点M对应的圆心角为θ/2 = π/3(即60度),根据弦长公式,AM = 2 5 sin((2π/3)/4) = 10 sin(π/6) = 10 0.5 = 5,弧的中位线长度为5。
需要注意的是,弧的中位线的长度不仅取决于圆的半径,还与弧的长度或圆心角有关,当弧的长度趋近于零时,弧的中位线长度也趋近于零;当弧的长度等于半圆时(即圆心角为π),弧的中位线长度为2r sin(π/4) = 2r (√2/2) = r√2,这些性质可以帮助我们更好地理解弧的中位线在不同情况下的变化。
弧的中位线在实际应用中也有广泛的用途,在建筑设计中,弧形结构的对称性和稳定性可以通过弧的中位线来分析;在物理学中,圆周运动的轨迹分析也可能涉及弧的中位线的计算,掌握弧的中位线的求解方法对于解决实际问题具有重要意义。

为了更清晰地展示弧的中位线长度与圆心角和半径的关系,我们可以通过以下表格来总结不同圆心角下的弧的中位线长度(假设半径r = 1):
| 圆心角θ(弧度) | 弧的中位线长度(2r * sin(θ/4)) |
|---|---|
| π/2 | 2 * sin(π/8) ≈ 0.765 |
| 2 * sin(π/4) ≈ 1.414 | |
| 3π/2 | 2 * sin(3π/8) ≈ 1.848 |
| 2π | 2 * sin(π/2) = 2 |
从表格中可以看出,随着圆心角的增大,弧的中位线长度也逐渐增大,这与几何直觉是一致的。
我们需要注意弧的中位线与弧的弦之间的关系,弧的弦AB的长度可以通过公式AB = 2r sin(θ/2)计算,而弧的中位线长度为2r sin(θ/4),由于sin(θ/4) < sin(θ/2)(对于0 < θ < π),因此弧的中位线长度小于弦的长度,这一性质在几何证明和计算中经常被用到。
求弧的中位线需要明确弧的中点定义,计算圆心角,并利用弦长公式求解中位线长度,通过具体的例子和表格,我们可以更直观地理解弧的中位线的性质及其变化规律,掌握这一方法不仅有助于解决几何问题,还能为后续学习更复杂的曲线性质奠定基础。
相关问答FAQs:
-
问:弧的中位线与弦的中位线有什么区别?
答:弧的中位线是连接弧的两个端点与弧的中点所形成的线段,而弦的中位线是连接弦的两个端点与弦的中点的线段,弧的中位线涉及弧的几何性质,而弦的中位线仅与弦的长度有关,弧的中位线长度通常小于弦的长度,因为弧的中点位于圆周上,而弦的中点位于弦的内部。 -
问:如何判断弧的中位线是否为圆的直径?
答:弧的中位线是否为圆的直径取决于弧的长度,当弧的长度等于半圆时(即圆心角为π弧度),弧的中点位于圆周上与弧的两个端点形成直角的位置,此时弧的中位线长度为r√2,不等于直径2r,只有当弧的长度等于整个圆周时(即圆心角为2π弧度),弧的中位线才可能成为直径,但此时弧的两个端点重合,中位线退化为一个点,弧的中位线通常不会成为圆的直径。