青春,这个充满活力与可能性的生命阶段,常常被诗人用华丽的辞藻描绘,被艺术家用绚烂的色彩勾勒,当我们试图用一种更精确、更抽象的语言来表达它时,数学公式或许能提供一种独特而深刻的视角,数学,作为宇宙的语言,其简洁的符号与严谨的逻辑,竟能与青春的复杂与多变产生奇妙的共鸣,下面,我们将从几个不同的维度,尝试用数学公式来拆解与表达“青春”这一概念。

我们可以从最基础的函数关系入手,青春的活力与成长,可以用一个指数增长函数来描绘,设时间为自变量 t(t ≥ 0),代表从青春期开始算起的岁月;青春的活力、学识或技能水平为因变量 E(t),E(t) = E₀ * e^(kt) 便是一个极佳的模型,E₀ 是初始值,代表个体进入青春期时的基础状态;e 是自然常数,象征着一种不可抗拒的、源于生命本身的增长动力;k 是增长系数,它因人而异,代表着个体的天赋、努力程度与环境机遇的综合作用,在青春的初期,这个函数图像呈现出近乎垂直的陡峭上升,象征着知识爆炸式增长、体能达到巅峰、世界观迅速形成的时期,每一天都充满了新的可能,每一次努力都能带来显著的回报,这种“复利效应”般的成长,正是青春最耀眼的特征之一。
青春并非只有一往无前的增长,它同样伴随着探索的迷茫与试错的成本,这时,一个带有波动项的函数或许更为贴切,我们可以将青春的整体状态 S(t) 表达为:S(t) = A(t) + Bsin(ωt + φ),在这个公式中,A(t) 代表了上述的指数增长趋势,是青春的主旋律;而 Bsin(ωt + φ) 则叠加了一个周期性的波动,B 是波动的振幅,代表着个体情绪或状态波动的剧烈程度;ω 是角频率,反映了波动的快慢,青春期的情绪可能像过山车一样,时而高涨,时而低落;φ 是初相位,代表着个体在特定时间点上的独特心境,这个公式告诉我们,青春是在总体向上的趋势中,伴随着无数次的成功与失败、喜悦与悲伤的螺旋式上升,那些深夜里的辗转反侧,考试后的欣喜若狂,与朋友争吵后的懊恼,以及重归于好的温暖,都被这个正弦波精确地记录下来,共同构成了青春完整的“心电图”。
更进一步,青春的选择与未来的轨迹,可以用概率论与统计学的语言来阐述,人生在每一个十字路口,都像是一次随机试验,我们可以用概率分布函数 P(x) 来描述个体在某个时间点 t,选择不同道路 x 的可能性,P(继续深造)、P(选择职业A)、P(搬迁到城市B) 等,青春的宝贵之处,正在于其概率分布的“高方差”,与中年后相对确定的路径不同,青春期的选择充满了不确定性,每一种结果的概率分布都较为分散,意味着拥有更多的可能性,每一次尝试,无论成功与否,都在更新这个概率分布,通过贝叶斯定理,不断修正对未来可能性的认知,青春可以被看作是一个信息收集和概率收敛的过程,勇敢地去尝试,就是去探索这个分布的广度;而每一次反思与总结,则是让这个分布的峰值变得更加清晰,最终指向一个更明确的人生方向。
从更宏观的视角看,青春的群体效应,可以用微积分中的“导数”与“积分”来理解,一个社会或时代的青春活力,可以看作是所有个体青春能量的总和,其瞬时变化率,即 dE_total/dt,代表了这个时代发展的速度与加速度,如果这个导数为正且数值很大,说明整个社会处于高速发展的青春期,充满了创新与变革的力量,而青春的总价值,则可以通过对个体能量函数 E(t) 在时间区间 [t₁, t₂] 上进行积分来得到,即 ∫[t₁, t₂] E(t) dt,这个积分值代表了青春这段时期所创造的总知识、总体验、总情感和总贡献,它不仅仅是终点值的函数,更是对整个过程的累积,一个短暂但极其辉煌的青春,和一个漫长而平稳的青春,可能拥有相同的积分值,但它们的“能量密度”曲线形状截然不同。
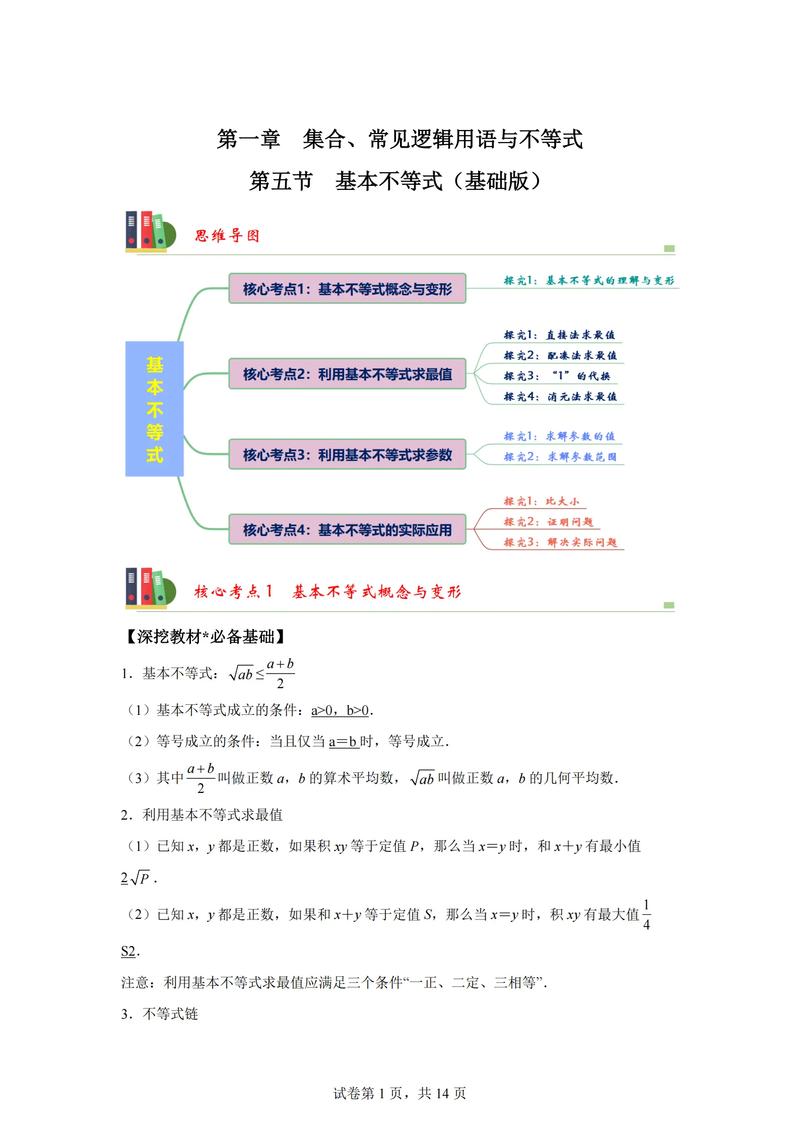
为了更直观地理解这些抽象的公式,我们可以用一个表格来对比它们所描述的青春的不同侧面:
| 数学公式/概念 | 表达的青春内涵 | 核心特征解读 |
|---|---|---|
| 指数增长函数 E(t) = E₀ * e^(kt) | 活力、学识、技能的飞速成长 | 复利效应、不可逆的上升趋势、个体差异体现在系数 k 上 |
| 波动函数 S(t) = A(t) + B*sin(ωt + φ) | 情绪的起伏、探索的曲折、试错的过程 | 在主旋律 A(t) 下的周期性波动,B 代表情绪波动幅度,ω 代表波动频率 |
| 概率分布函数 P(x) | 人生选择的不确定性、未来的多种可能性 | 分布的“高方差”是青春的标志,每一次尝试都在更新对未来的认知 |
| 导数 dE_total/dt | 时代发展的速度与活力 | 正且大的导数值代表社会处于高速发展的“青春期” |
| 积分 ∫E(t)dt | 青春期的总价值与总贡献 | 对过程的累积,衡量一段生命历程的深度与广度 |
青春并非一个无法言说的模糊概念,它可以是指数函数中那股喷薄而出的生命力,是波动函数里那真实而起伏的心跳,是概率分布图上那无限延伸的未来可能,也是导数与积分所描绘的时代洪流与个体价值,数学公式以其独特的冷静与精确,为我们揭示了青春背后深刻的结构与规律,它告诉我们,青春不仅是一段感性的岁月,更是一段可以被理性分析、被深刻理解的旅程,它既有其内在的、不可抗拒的增长逻辑,也充满了个体化的情感波澜与充满无限可能的选择空间,用数学的眼光看青春,我们看到的不仅是浪漫,更是一种秩序之美,一种力量之美,一种在不确定性中奔向确定性的、充满希望的美。
相关问答FAQs
为什么说用数学公式表达青春会显得“冷酷”,失去了青春的温度? 解答: 这种担忧是可以理解的,因为数学本身是抽象和客观的,而青春充满了主观的情感和温度,用数学公式表达青春并非为了取代感性的描述,而是为了提供一种全新的、补充性的视角,这些公式并非要定义青春,而是要“建模”青春的某些侧面,指数增长函数描绘了成长的“势能”,波动函数则量化了情绪的“起伏”,这些模型恰恰为那些感性的体验找到了一种理性的骨架,它们帮助我们理解,那些看似混乱的情绪波动和飞速的成长背后,可能存在着某种可以被理解的规律,数学公式非但不会失去温度,反而像是为青春的炽热火焰找到了一个稳定的炉膛,让我们能更清晰地观察和欣赏它的光芒,它是一种深度的解读,而非表面的替代。

青春的“高方差”概率特性,是否意味着我们应该鼓励年轻人“盲目试错”? 解答: 绝对不是,青春的“高方差”指的是选择可能性的广泛,而非鼓励无头绪的“瞎碰”,恰恰相反,认识到这一点,更要求我们进行“有策略的试错”,概率论告诉我们,每一次尝试都是一次获取信息、更新认知(即更新我们的概率分布模型)的机会,试错不应是盲目的,而应是带有学习目的的,在尝试之前,我们可以通过学习、咨询等方式,为我们的初始概率分布 P(x) 赋予一个更合理的“先验知识”,这能让我们更有可能选择那些成功概率更高的选项进行尝试,在尝试之后,必须进行深入的复盘,分析成功或失败的原因,从而有效地修正我们的模型,青春的高方差特性,要求我们既要有拥抱不确定性的勇气,也要有从每一次经历中学习的智慧,让每一次“试错”都成为通往更清晰未来的一块坚实铺路石,而不是原地打转的徒劳消耗。