18加21如何破十法是一种针对两位数加法运算的简便计算方法,特别适合小学低年级学生或数学初学者快速掌握进位加法的技巧,破十法的核心思想是将其中一个加数拆分成“十”和“个位”两部分,利用“凑十法”的原理简化计算过程,从而将复杂的进位加法转化为简单的加减组合运算,下面将从原理、步骤、实例分析、常见误区及练习建议五个方面详细展开说明。
破十法的核心原理
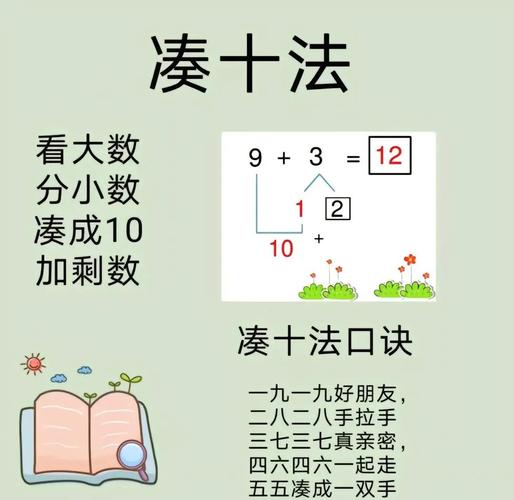
破十法的本质是利用十进制数的位值概念,通过“拆数”和“凑十”两个关键步骤将加法运算分解,其基本原理基于加法交换律和结合律,即通过调整加数的位置和组合,使计算过程更符合口算习惯,在计算18+21时,可以选择将18拆分为“10”和“8”,或将21拆分为“20”和“1”,但更优的策略是拆分其中一个加数,使其与另一个加数的个位数凑成“十”,从而减少进位带来的复杂性,这种方法不仅适用于两位数加法,也可以扩展到三位数或更复杂的加法运算中,是培养数感和运算能力的重要工具。
详细步骤与操作流程
以18+21为例,破十法的具体操作步骤如下:
-
选择拆分对象:观察两个加数,选择个位数较大或与另一个加数的个位数相加能凑“十”的数进行拆分,18的个位数是8,21的个位数是1,8+1=9,无法直接凑十,因此可拆分十位数较大的18(或21),这里选择拆分18,将其分为“10”和“8”。
-
重新组合算式:将原算式18+21转化为(10+8)+21,利用加法结合律重组为10+(8+21),但这样并未简化计算,因此更合理的拆分方式是将18拆分为“10”和“8”后,先计算8+21的个位部分,再与十位数相加。
 (图片来源网络,侵删)
(图片来源网络,侵删) -
计算个位数并凑十:计算8+21的个位数部分,即8+1=9,此时无需进位,因此可直接得到个位数为9,十位数为2(来自21的十位)与1(来自18的十位)的和,即2+1=3,最终结果为39,但这种方法未体现“破十”的核心,因此更标准的破十法步骤如下:
- 拆分加数:将18拆分为“10”和“8”,原算式变为10+8+21。
- 分组计算:先计算8+21=29,再计算10+29=39,这种方法虽然正确,但未充分利用“凑十”原理。
更优的破十法操作应为:选择拆分21,将其分为“20”和“1”,然后计算18+1=19,再19+20=39,这样通过先加个位数再整十数,避免了复杂的进位处理。
-
验证结果:通过传统竖式加法验证:18+21=39,确认结果正确。
实例分析与对比
为了更直观地理解破十法的优势,以下通过表格对比传统方法与破十法的计算效率:

| 计算方法 | 步骤 | 计算过程 | 优点 | 缺点 |
|---|---|---|---|---|
| 传统竖式法 | 个位相加,十位相加,处理进位 | 8+1=9,1+2=3,结果39 | 逻辑清晰,适合所有情况 | 需要书写,进位易出错 |
| 破十法(拆18) | 拆分18为10和8,分步计算 | 10+8+21=10+29=39 | 减少进位,口算简便 | 拆分后步骤较多 |
| 破十法(拆21) | 拆分21为20和1,先加个位数再加整十数 | 18+1=19,19+20=39 | 步骤少,适合个位数较小的情况 | 需要灵活选择拆分对象 |
从表格可以看出,破十法的关键在于合理拆分加数,使计算过程更符合口算习惯,在18+21中,拆分21为20和1,先计算18+1=19(无需进位),再19+20=39,仅需两步即可完成,比传统竖式法更高效。
常见误区与注意事项
-
拆分对象选择不当:若选择拆分个位数较大的数(如18的8),可能导致无法凑十,反而增加计算难度,拆分18为10和8后,计算8+21时仍需进位,违背了破十法的简化初衷,正确做法是优先拆分个位数较小的加数,或选择与另一个加数个位数相加能凑“十”的数。
-
忽略运算顺序:破十法需要严格按照“先加个位数,再加整十数”的顺序进行,若顺序颠倒(如先算10+21=31,再31+8=39),虽然结果正确,但步骤未简化,失去破十法的意义。
-
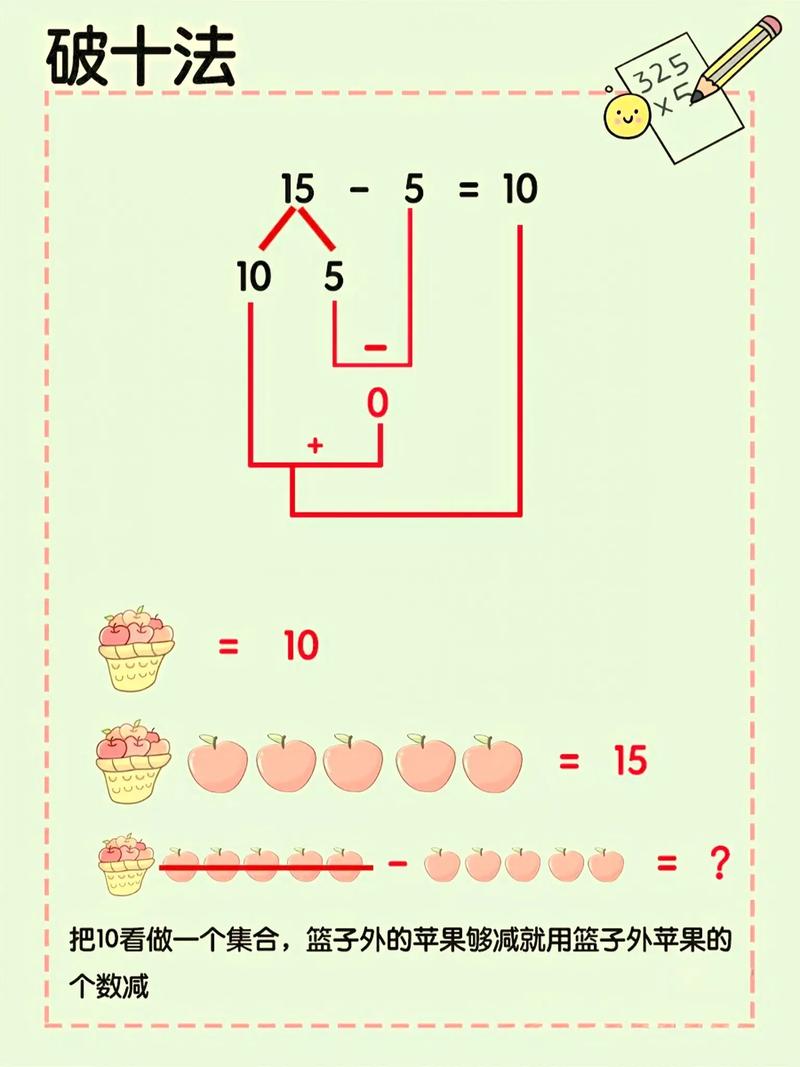
进位处理错误:在拆分后计算时,若个位数相加超过十,仍需处理进位,计算17+23时,若拆分17为10和7,计算7+23=30,再10+30=40,此时无需进位;但若计算19+23,拆分19为10和9,9+23=32,再10+32=42,仍需注意32的十位数与10相加时的进位。
练习建议与拓展应用
为熟练掌握破十法,建议学生通过以下方式练习:
- 基础拆分练习:从简单的两位数加法开始,如25+36,尝试拆分其中一个加数,优先选择个位数较小的数(如25拆为20和5),计算5+36=41,再20+41=61。
- 凑十专项训练:设计个位数相加凑“十”的题目,如28+32(拆分28为20和8,8+32=40,20+40=60),强化凑十意识。
- 生活场景应用:在购物、计算时间等场景中运用破十法,如计算12元+19元,拆分19为10和9,12+9=21,21+10=31元,提升实际应用能力。
破十法还可拓展到减法运算(如破十减法)和多位数加法,例如计算123+456时,可拆分123为100+20+3,分步与456相加,进一步培养数感。
相关问答FAQs
问题1:破十法与凑十法有什么区别?
解答:破十法和凑十法都是简化加法运算的方法,但适用场景不同,凑十法主要用于20以内的加法,如8+5,将5拆分为2和3,先算8+2=10,再10+3=13;而破十法主要用于两位数及以上的加法,通过拆分加数减少进位复杂度,两者的共同点是利用“十”作为中间桥梁,但破十法更强调对较大数的拆分处理。
问题2:如何判断是否适合使用破十法?
解答:破十法适用于两个加数均为两位数,且至少一个加数的个位数较小(如1-5)的情况,计算27+34时,拆分27为20和7,7+34=41,20+41=61,效率较高;但若计算89+97,由于个位数较大且相加需进位,破十法可能不如传统竖式法简便,此时应根据具体数字灵活选择方法,避免生搬硬套。