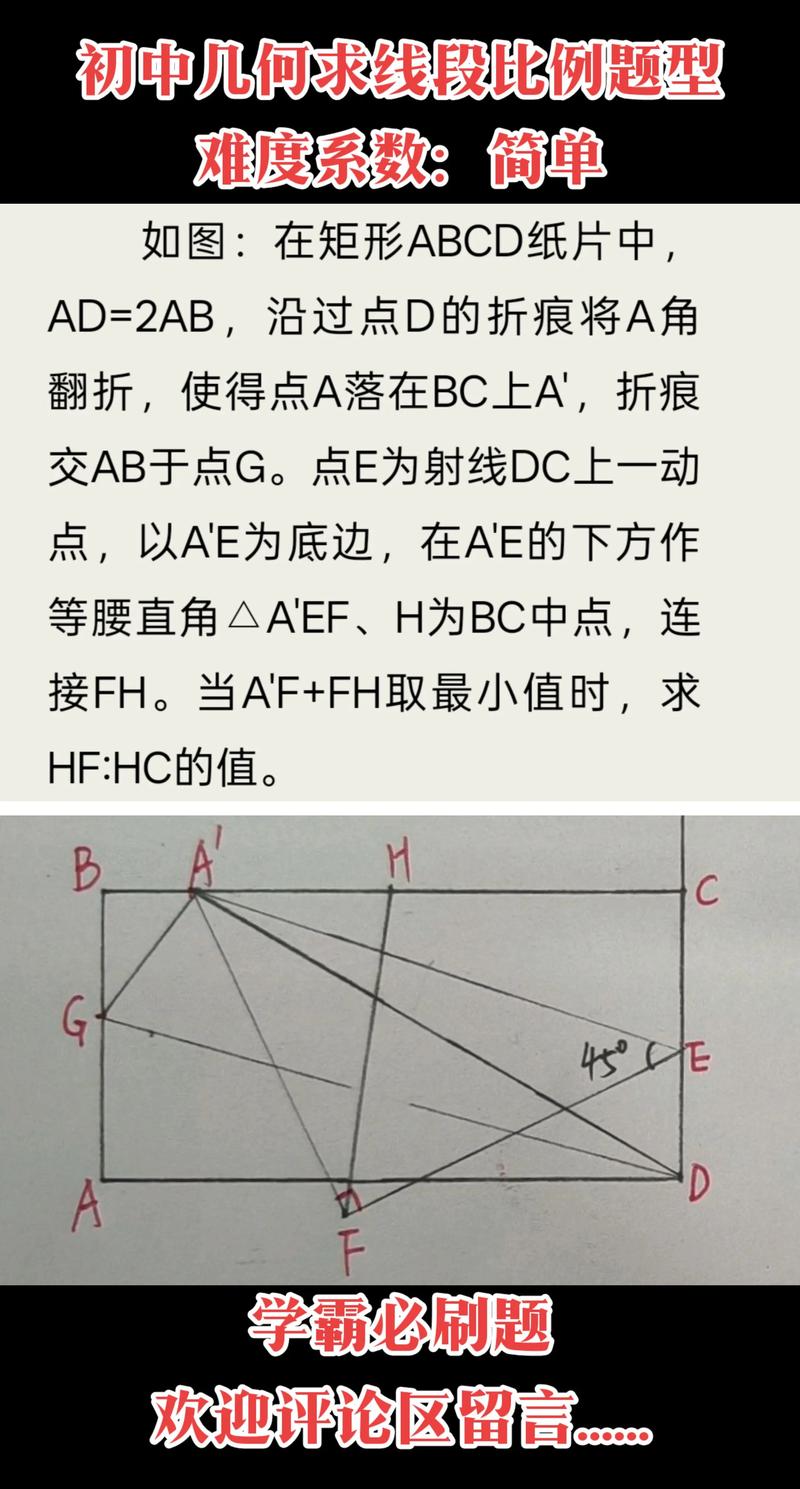
运用成比例线段解题是几何学中的重要方法，其核心在于利用线段之间的比例关系推导未知量，常涉及相似三角形、平行线分线段成比例定理等基础理论，以下从理论基础、常见模型、解题步骤及实例分析四个方面展开详细说明，并通过表格归纳关键知识点,最后附相关问答。
理论基础与核心定理
成比例线段的理论基础主要包含以下定理：
- 平行线分线段成比例定理：三条平行线被两条直线所截，所得的对应线段成比例，如图1，若l₁∥l₂∥l₃，则AB/BC=DE/EF。
- 相似三角形的性质：相似三角形中，对应边成比例，对应高、中线、角平分线等也成比例，若△ABC∽△A'B'C'，则AB/A'B'=BC/B'C'=AC/A'C'。
- 角平分线定理：三角形内角平分线分对边所得的两条线段与邻边成比例，如图2，在△ABC中，若AD是∠BAC的平分线，则BD/DC=AB/AC。
- 直角三角形的射影定理：直角三角形中，斜边上的高是两条直角边在斜边上的射影的比例中项，即AD²=BD·DC（如图3，∠ACB=90°，CD⊥AB）。
常见解题模型与技巧
-
“A字形”与“X字形”模型
- A字形：如图4，若DE∥BC，则AD/AB=AE/AC=DE/BC，常用于构造平行线转移比例。
- X字形：如图5，若AC与BD相交于点O，且AB∥CD，则AO/OC=BO/OD，适用于证明线段比例关系。
-
相似三角形的构造
当题目中涉及平行线或共边共角时，可通过添加辅助线构造相似三角形，在梯形ABCD中，AD∥BC，可过点D作DE∥AB交BC延长线于E，构造△ADE与△ABC相似。
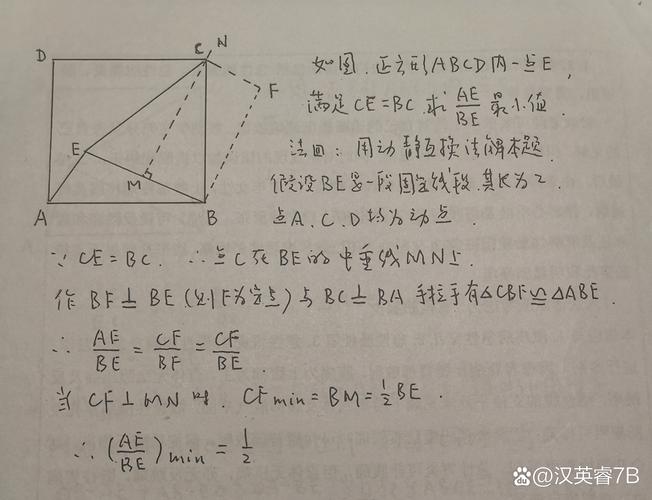（图片来源网络，侵删） -
比例转换与等积代换
利用比例的性质（合比定理、等比定理）进行转换，如若a/b=c/d，则(a+b)/b=(c+d)/d；或通过中间比传递，如AB/CD=MN/PQ，PQ/RS=UV/WX，则AB/CD=UV/WX。
解题步骤与实例分析
解题步骤：
① 审题与构图：明确已知条件，标注比例关系，绘制图形；
② 选定理：根据平行线、角平分线、直角三角形等特征选择合适定理；
③ 列比例式：将已知量与未知量代入比例关系；
④ 解方程：通过代数方法求解未知量；
⑤ 验证：检查比例关系是否合理,单位是否统一。
实例分析：
例题：在△ABC中，D为BC边上一点，BD=3，DC=2，E为AC上一点，且DE∥AB，AE=4，求EC的长度。
解析：
① 由DE∥AB，根据平行线分线段成比例定理，得AD/DB=AE/EC；
② 代入已知数据，AD/3=4/EC；
③ 需求AD，由BD=3、DC=2，得BC=5，但AD未知，需补充条件（若题目给出AD长度或另一比例关系）； 补充AD=6，则6/3=4/EC，解得EC=2。
注：实际解题中需根据题目条件灵活调整，若AD未知，可通过其他比例关系（如角平分线或相似三角形）间接求解。
关键知识点归纳表
| 定理/模型 | 适用场景 | |
|---|---|---|
| 平行线分线段成比例 | 三平行线截两直线，对应线段成比例 | 题目中存在平行线时 |
| 相似三角形性质 | 对应边成比例，对应线段（高、中线等）成比例 | 证明线段比例或求长度 |
| 角平分线定理 | 内角平分线分对边与邻边成比例 | 涉及角平分线时 |
| 射影定理 | 直角三角形中，斜边高=两直角边射影的比例中项 | 直角三角形斜边上的高问题 |
| A字形/X字形模型 | 利用平行线构造比例关系 | 梯形、相交直线等图形 |
相关问答FAQs
问题1：如何判断题目中是否可以使用成比例线段解题？
解答：当题目中出现以下特征时，可优先考虑成比例线段：① 图形中存在平行线（尤其是与截线相交）；② 涉及三角形的角平分线或高；③ 需要求线段长度或比例关系，且直接计算困难；④ 题目明确给出比例条件（如“AB:CD=2:3”），若图形可通过添加辅助线构造相似三角形或平行线,也可尝试此方法。
问题2：在使用成比例线段时，如何避免比例对应错误？
解答：比例对应错误是常见失误，需注意以下三点：① 顺序一致性：分子分段的顺序需一致，如AD/DB=AE/EC，不可写成AD/DB=EC/AE；② 图形标注：在图形中明确标注对应点（如A对应D，B对应E），避免混淆；③ 验证单位：若比例涉及长度，确保单位统一；④ 特殊值检验：通过假设特殊值（如令某线段长度为1）验证比例关系是否成立，在相似三角形中，可先计算已知边的比例,再验证未知边是否符合相同比例。
