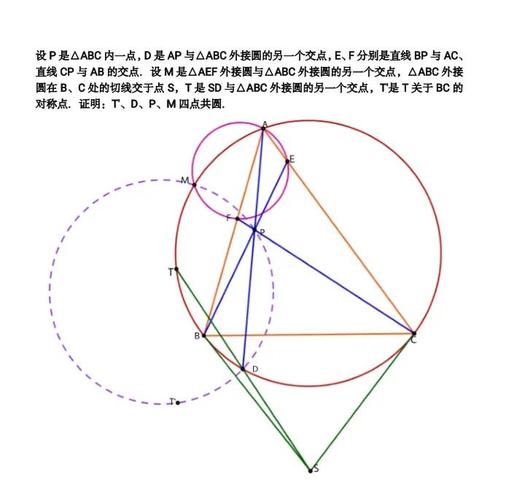
要确定四点共圆的圆心,首先需要明确四点共圆的条件,即四个点位于同一个圆上,圆心到这四个点的距离相等,因此圆心实际上是这四个点所构成的四边形的外接圆圆心,以下是详细的步骤和方法:

验证四点共圆
在寻找圆心之前,必须先确认四点是否共圆,常用的方法包括:
- 对角互补法:若四边形的一组对角互补(和为180°),则四点共圆。
- 距离法:计算四个点中任意三点确定的圆的方程,验证第四点是否满足该方程。
- 幂的相等性:若四个点中任意一点对其他三点的幂相等,则四点共圆。
确定圆心的方法
若四点共圆,圆心可以通过以下方法确定:
(1)垂直平分线交点法
- 步骤:
- 选取四点中的任意两点(如A、B),连接AB,作AB的垂直平分线。
- 选取另外两点(如C、D),连接CD,作CD的垂直平分线。
- 两条垂直平分线的交点即为圆心。
- 原理:圆心到任意两点的距离相等,因此圆心必在两点连线的垂直平分线上,两条垂直平分线的交点满足到四点的距离相等。
- 注意事项:若四点共线,则无解;若垂直平分线平行或重合,需重新选择点对。
(2)圆的方程法
- 步骤:
- 设圆心坐标为((a, b)),半径为(r),圆的方程为((x-a)^2 + (y-b)^2 = r^2)。
- 将四点坐标((x_1,y_1))、((x_2,y_2))、((x_3,y_3))、((x_4,y_4))代入方程,得到四个方程。
- 选取其中三个方程解出(a, b, r),验证第四个方程是否成立。
- 原理:圆心坐标满足所有四点的距离公式,通过解方程组可求得圆心。
- 适用场景:适用于坐标已知的四点,计算量较大但通用性强。
(3)几何性质法
- 步骤:
- 若四边形为矩形或等腰梯形,圆心为对角线交点。
- 若四边形为菱形,圆心为对角线交点(需验证是否共圆)。
- 原理:利用特殊四边形的对称性,圆心位于对角线交点。
- 局限性:仅适用于特殊四边形。
(4)向量法
- 步骤:
- 设四点为(A, B, C, D),向量(\overrightarrow{OA}, \overrightarrow{OB}, \overrightarrow{OC}, \overrightarrow{OD})。
- 圆心(O)满足(|\overrightarrow{OA}| = |\overrightarrow{OB}| = |\overrightarrow{OC}| = |\overrightarrow{OD}|)。
- 通过向量模长相等建立方程求解。
- 原理:向量的模长代表距离,圆心到四点的距离相等。
- 适用场景:适用于向量运算方便的情况。
计算示例
假设四点坐标为(A(1,1))、(B(2,-1))、(C(-1,0))、(D(0,2)),验证共圆并求圆心:
- 验证共圆:
- 计算三点A、B、C的圆心:
- AB中点((1.5,0)),斜率(-2),垂直平分线斜率(0.5),方程(y = 0.5(x-1.5))。
- BC中点((0.5,-0.5)),斜率(-1),垂直平分线斜率(1),方程(y+0.5 = x-0.5)。
- 联立解得圆心((1,0)),半径(\sqrt{2})。
- 验证D点:((0-1)^2 + (2-0)^2 = 5 \neq 2),不共圆(需重新选择点或检查计算)。
- 计算三点A、B、C的圆心:
常见错误与注意事项
- 未验证共圆:直接计算可能导致无解或错误。
- 垂直平分线选择不当:若所选两点连线与另两点连线平行,需更换点对。
- 计算错误:解方程或几何作图时需仔细检查。
确定四点共圆的圆心,核心是找到到四点距离相等的点,垂直平分线交点法直观易操作,圆的方程法通用性强,几何性质法适用于特殊图形,实际应用中需根据已知条件选择合适方法,并确保四点共圆的前提。
相关问答FAQs
Q1: 四点共圆的圆心是否唯一?
A1: 是的,若四点共圆且不共线,则圆心唯一,若四点共线,则无圆心(或视为无穷远点),若四点中有三点共线,则四点不可能共圆(除非四点全部共线)。
Q2: 如何快速判断四点是否共圆?
A2: 快速判断方法包括:
- 观察对角是否互补(适用于四边形);
- 计算任意三点确定的圆,验证第四点是否在圆上(适用于坐标已知的情况);
- 利用幂的定理:若四点中任意一点对其他三点的幂相等,则共圆。