快速记住公式“v=s/t”(速度等于路程除以时间),关键在于理解其物理意义、建立直观联系,并通过多样化的方法强化记忆,以下是详细的策略和步骤:

拆解公式的本质
首先明确每个符号的含义:
✅ v代表“速度”(Velocity),描述物体运动的快慢程度;单位通常是米/秒(m/s)或千米/小时(km/h)。
✅ s是“位移”或“路程”(Distance),指物体实际经过的路径长度;注意与矢量性的位移区分时需结合方向讨论。
✅ t为“时间”(Time),即完成这段运动所消耗的时间间隔。
公式的核心逻辑在于:单位时间内通过的路程越长,则速度越快,若某人用2小时走了10公里,那么他的速度就是每小时5公里(v=10km÷2h=5km/h),这种从生活场景出发的例子能帮助你将抽象符号转化为具体经验。
| 物理量 | 英文缩写 | 定义 | 常见单位 | 示例 |
|---|---|---|---|---|
| 速度 | v | 单位时间的位移变化量 | m/s, km/h | 汽车仪表盘显示80km/h |
| 路程 | s | 运动轨迹的总长度 | m, km | 马拉松全程约42km |
| 时间 | t | 持续的运动时长 | s, min, h | 煮一碗面需要10分钟 |
多维度记忆技巧组合拳
🧠 联想法——构建故事画面
想象自己驾驶一辆跑车参加比赛🏆:赛道总长为s公里,计时器显示用了t分钟冲过终点线,此时裁判宣布你的平均速度是v=s/t,把数字代入试试:比如s=120km,t=2h → v=60km/h,这样的动态场景会让公式变得生动,而非死记硬背的文字组合。
✍️ 手写推导过程
动手写下完整的推理链条:已知某段时间内移动的距离为s,耗时t,求平均每秒钟前进多少米?自然得出v=s÷t,反复书写能加深肌肉记忆,尤其适合视觉型学习者,还可以尝试变换形式练习:由v=s/t可推出s=v·t、t=s/v,三者互为逆运算关系。
📊 表格对比法强化规律
制作不同情境下的数据对照表,观察变量间的比例关系:
| 情况 | 路程(s) | 时间(t) | 计算出的速度(v=s/t) | |
|------------|---------|---------|--------------------|-------------------------------|
| A车匀速行驶| 300m | 60s | 5m/s | 固定值说明匀速直线运动 |
| B步行上班 | 1.5km | 0.5h | 3km/h | 换算单位不影响本质结果 |
| C火箭加速 | 随时间增加而增大 | — | — | 此阶段不能用该公式直接计算瞬时速度 |

通过填充表格发现:当s增大而t不变时,v必然增大;反之若t延长但s不变,则v减小,这种量化分析有助于掌握变量间的制约关系。
🔍 错题归因训练
收集作业或试卷中涉及此公式的错误案例,分类整理常见误区:
✘ 混淆时刻与时间段:误将起始时刻当作总耗时(如把8:00当成了Δt);
✘ 忽略单位统一性:未将分钟转为小时就直接计算导致数量级错误;
✘ 张冠李戴公式:把加速度a=(v₂−v₁)/t错用于求平均速度的问题中,针对弱点专项突破,能有效避免重复犯错。
应用场景实战演练
📌 例题1:基础应用 “一辆自行车从家到学校的距离是4.5千米,骑行时间为半小时,求平均速度。”
解析步骤:①确认已知量s=4.5km,t=0.5h;②套用公式v=s/t=4.5÷0.5=9km/h;③检验合理性——符合日常骑车经验范围(通常10~20km/h左右)。
📌 例题2:复杂变式
进阶问题:“若前半程以v₁行驶,后半程以v₂行驶,全程的平均速度是多少?”此时需先设总路程为2s,分别计算两段所用时间t₁=s/v₁、t₂=s/v₂,再由总时间T=t₁+t₂得到平均速度V_avg=2s/(s/v₁ + s/v₂)=2v₁v₂/(v₁+v₂),这类综合题型能检验你是否真正吃透了原始公式的内涵。
跨学科联结拓展认知边界
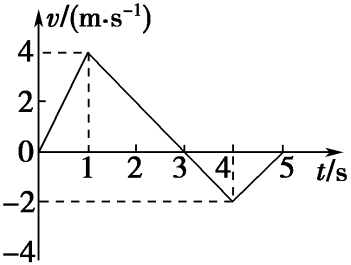
将数学中的正反比函数图像引入物理学领域:绘制v-t图时,若物体做匀速直线运动,图像应呈现水平直线;而在s-t图中则表现为倾斜向上的直线,斜率恰等于速度大小,这种几何视角下的解读方式,可借助坐标系工具实现代数与图形的双重验证,在经济学里也有类似概念——“边际产出效率”,本质上都是对比率关系的量化研究。
定期复习与自我检测机制
建议采用艾宾浩斯遗忘曲线制定的复习计划:首次学习后间隔5分钟、30分钟、12小时各复述一遍公式;次日早晨再次默写并举例验证;一周后进行章节小结测试,利用闪卡App设置随机抽查模式,系统会自动根据你的答题正确率调整后续复习频率,每次成功回忆都能增强神经突触连接强度,最终形成长期稳定的知识锚点。
FAQs
Q1: 如果题目只给出起点和终点坐标,如何确定适用哪个公式?
A: 当物体沿直线单向运动且无往复时,可直接使用v=s/t;但如果存在折返情况(如来回跑步),则需要分段计算各段路程对应的时间后再取加权平均值,关键是要先判断运动性质是否符合“单一方向上的连续位移”。
Q2: 为什么不能说“速度就是距离除以时间”?必须强调是“位移”吗?
A: 物理学中的“速度”是矢量,既有大小又有方向,因此理论上应该用位移除以时间;而日常口语中的“速率”才是标量版的路程除以时间,不过初中阶段常简化处理,只要题目未涉及方向变化,两者结果数值相同,但在大学力学课程中