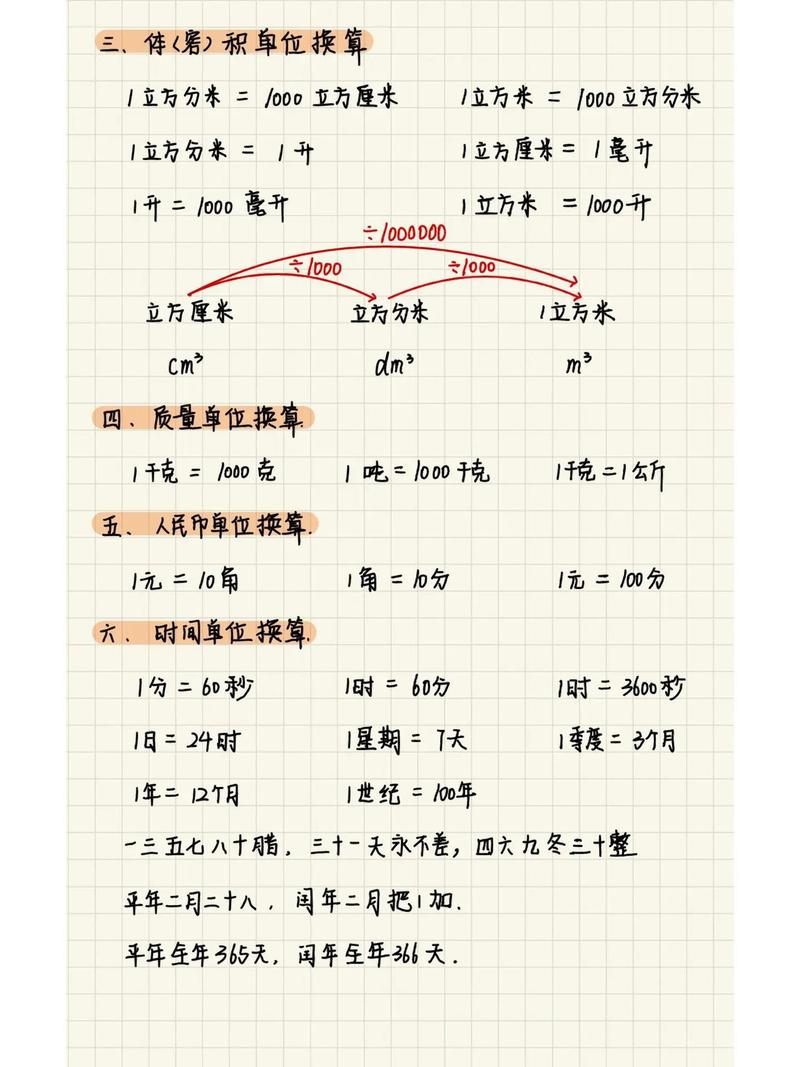
在数学计算和日常生活中,单位换算与计算是不可或缺的技能,而“巧算”单位不仅能提高效率,还能减少错误,所谓“巧算”,并非依赖死记硬背,而是通过理解单位间的关系、掌握规律和方法,实现快速准确的计算,以下从单位体系、换算原理、实用技巧及常见误区等方面,详细解析如何巧算计算单位。

理解单位体系:巧算的基础
单位是衡量事物量纲的标准,国际单位制(SI)中,基本单位包括米(长度)、千克(质量)、秒(时间)、安培(电流)、开尔文(温度)、摩尔(物质的量)、坎德拉(发光强度)7个,其他单位由基本单位导出,速度的单位“米/秒”由长度和时间单位组合而成,巧算单位的前提是熟悉常用单位的体系归属,明确“哪些单位属于同一类量纲”,避免将长度、质量等不同量纲的单位混淆。“吨”和“千克”都是质量单位,可以换算;而“米”和“秒”属于不同量纲,无法直接换算,日常生活中还涉及非国际单位制单位,如“斤”“亩”“公里”等,需了解其与国际单位的换算关系(如1公里=1000米,1斤=0.5千克)。
掌握单位换算的核心原理:进率与方向
单位换算的本质是“乘以或除以进率”,而进率是单位间的倍数关系,确定进率是巧算的关键:
- 十进制单位:国际单位制中的多数单位为十进制,进率为10、100、1000等,便于口算,长度单位“千米→米→分米→厘米→毫米”,相邻单位进率为10;质量单位“吨→千克→克”,相邻单位进率为1000。
- 非十进制单位:部分单位进率特殊,需重点记忆,时间单位“1小时=60分钟,1分钟=60秒”(进率60);“1个月=28/29/30/31天”(需注意月份差异);角度单位“1度=60分,1分=60秒”(进率60)。
- 复合单位:由多个基本单位组合而成,换算时需分别处理每个分量,速度单位“千米/小时”换算为“米/秒”,需将“千米”换算为“米”(×1000),“小时”换算为“秒”(×3600),整体为“×1000÷3600=×5/18”。
换算方向:根据“大单位→小单位乘进率,小单位→大单位除以进率”的规则,避免混淆,1.5千克=1500克(小单位,乘1000);500米=0.5千米(大单位,除以1000)。
实用巧算方法与技巧
口诀与联想记忆法
对于特殊进率的单位,可通过口诀或联想快速记忆。
- 时间单位:“小时分秒六十进制,年月日要特殊记”(平年2月28天,闰年2月29天,大月31天,小月30天)。
- 面积单位:“平方进率是百方,公顷平方万进量”(1平方米=100平方分米,1公顷=10000平方米)。
- 质量单位:“吨与千克千进位,斤与千克半相连”(1吨=1000千克,1斤=0.5千克)。
分步拆解法
复杂单位换算可拆分为多个简单步骤,逐步完成,将“36千米/小时”换算为“米/秒”:
- 第一步:拆分复合单位为“36千米÷1小时”;
- 第二步:千米→米:36×1000=36000米;
- 第三步:小时→秒:1×3600=3600秒;
- 第四步:计算结果:36000米÷3600秒=10米/秒。
基准单位法
选择一个“基准单位”作为中间桥梁,统一换算,日常生活中“斤”与“公斤”的换算,可先统一为“千克”:1斤=0.5千克,2斤=1千克,3斤=1.5千克,避免直接记忆“斤”与“公斤”的倍数关系。
估算与验证法
通过估算快速判断结果合理性,减少计算错误,计算“1.2吨=多少千克”,1吨=1000千克,1.2吨应略大于1200千克,若结果为120千克,明显偏小,需重新检查进率。
表格法:常用单位换算速查表
为方便记忆,以下是部分常用单位的换算关系表:

| 量纲 | 单位名称 | 符号 | 换算关系 |
|---|---|---|---|
| 长度 | 千米 | km | 1 km = 1000 m |
| 米 | m | 1 m = 10 dm = 100 cm = 1000 mm | |
| 厘米 | cm | 1 cm = 10 mm | |
| 质量 | 吨 | t | 1 t = 1000 kg |
| 千克 | kg | 1 kg = 1000 g = 2 斤 | |
| 克 | g | 1 g = 1000 mg | |
| 时间 | 小时 | h | 1 h = 60 min = 3600 s |
| 分钟 | min | 1 min = 60 s | |
| 面积 | 平方千米 | km² | 1 km² = 1000000 m² |
| 平方米 | m² | 1 m² = 100 dm² = 10000 cm² | |
| 体积 | 立方米 | m³ | 1 m³ = 1000 dm³ = 1000000 cm³ |
| 升 | L | 1 L = 1 dm³ = 1000 mL | |
| 速度 | 千米/小时 | km/h | 1 km/h = 5/18 m/s ≈ 0.28 m/s |
| 米/秒 | m/s | 1 m/s = 3.6 km/h |
巧算单位的常见误区与规避
- 混淆进率:将“平方米”与“平方米”的进率误认为10(实际为100,因为1 m²=10 dm×10 dm=100 dm²),规避方法:明确“平方单位”“立方单位”的进率是基本单位进率的平方或立方(如1 m³=1000 dm³,进率10³=1000)。
- 忽略单位方向:“80厘米=多少米”,误将“厘米”→“米”乘以100(实际除以100),规避方法:用“大单位变小单位乘进率,小单位变大单位除以进率”口诀辅助判断。
- 复合单位漏算:“54 km/h换算为m/s”时,仅将千米换算为米,忽略小时换算为秒,规避方法:拆分复合单位,分别处理每个分量。
实际应用场景中的巧算
购物中的单位换算
购买商品时,常遇到“元/斤”与“元/千克”的换算,苹果5元/斤,相当于10元/千克(因为1斤=0.5千克,5元÷0.5 kg=10元/kg)。
出行中的速度单位
汽车仪表盘显示“km/h”,而行人速度常用“m/s”,限速60 km/h,换算为m/s为60×(5/18)≈16.67 m/s,即每秒移动约16.67米。
家庭装修中的面积计算
地板面积常用“平方米”,而瓷砖规格常用“厘米×厘米”,房间长5米(500厘米),宽4米(400厘米),若用80厘米×80厘米的瓷砖铺地,需瓷砖数量=(500÷80)×(400÷80)≈6.25×5=31.25块,向上取整32块。
相关问答FAQs
问1:如何快速记忆“平方米”与“平方分米”的进率?
答:可通过“画图法”理解:1平方米的正方形,边长为1米(10分米),面积=10分米×10分米=100平方分米,因此1平方米=100平方分米,同理,1立方米=1000立方分米(10分米×10分米×10分米),进率为10的立方。
问2:复合单位“千瓦时”(kW·h)换算为“焦耳”(J)时,如何巧算?
答:1千瓦时是功率1千瓦(1000瓦)的设备工作1小时(3600秒)所消耗的能量,因此1 kW·h=1000 W×3600 s=3.6×10⁶ J,记忆时只需记住“1 kW·h=3.6兆焦”,避免重复计算。



