断点回归命令(Regression Discontinuity Design, RDD)是一种准实验研究方法,主要用于评估当某个连续变量(即“ running variable ”或“ assignment variable ”)跨越特定阈值(即“ cutoff ”)时,结果变量是否发生显著变化,该方法的核心逻辑在于,由于个体在阈值附近的随机性,可以认为阈值两侧的个体除了是否跨越阈值外,其他特征是相似的,从而通过比较阈值附近两侧的样本差异来估计处理效应,断点回归命令在经济学、公共卫生、政治学等领域被广泛应用于政策评估、干预效果分析等场景,例如评估奖学金政策对学生成绩的影响、最低工资标准对就业率的作用等。

在实施断点回归分析时,研究者需要明确几个关键要素:首先是“ running variable ”,即用于分组的连续变量,如考试成绩、收入水平等;其次是“ cutoff ”,即决定个体是否接受处理的阈值,如考试分数线、贫困线等;最后是“ bandwidth ”,即阈值附近样本的选取范围,带宽的选择直接影响估计结果的准确性和稳健性,断点回归命令通常分为两类:精确断点回归(Sharp RDD)和模糊断点回归(Fuzzy RDD),精确断点回归中,个体跨越阈值后必然接受处理,处理状态是确定的;而模糊断点回归中,跨越阈值仅增加接受处理的概率,处理状态存在不确定性,此时需要借助工具变量法进行估计。
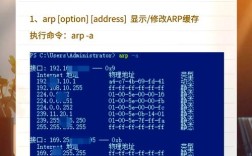
在实际操作中,断点回归命令的实现通常借助统计软件完成,以Stata为例,常用的命令包括rdrobust、rd和rdplot等。rdrobust命令提供了稳健的断点回归估计,支持多种带宽选择方法和核函数设定,能够处理异方差和潜在的相关性问题,使用rdrobust命令时,研究者需要指定“ running variable ”、“ cutoff ”以及结果变量,并通过bwselect选项选择带宽,kernel选项选择核函数(如三角核、Epanechnikov核等),为了验证断点回归的有效性,需要进行一系列稳健性检验,包括检验“ running variable ”在阈值两侧的分布是否连续(即是否存在操纵现象)、检验结果变量在阈值附近是否存在线性趋势、以及检验不同带宽下的估计结果是否稳健等,可以通过rdplot命令绘制“ running variable ”与结果变量的散点图及局部多项式拟合曲线,直观展示断点两侧的差异。
断点回归命令的优势在于其较强的内部有效性,即通过阈值附近的局部随机性解决了内生性问题,使得估计结果更接近因果效应,该方法也存在一定局限性,例如外部有效性可能受限,因为断点附近的样本特征可能无法推广到整个总体;带宽的选择对结果影响较大,若带宽过窄,可能导致样本量不足、估计精度降低;若带宽过宽,可能引入更多异质性样本,影响估计的准确性,研究者需要结合理论分析和数据特征,合理选择带宽,并进行充分的稳健性检验。
为了更直观地展示断点回归命令的应用,以下以一个假设的奖学金政策评估为例,说明关键参数的选择和结果解读,假设“ running variable ”为学生的入学考试成绩(满分100分),“ cutoff ”为60分,考试成绩≥60分的学生可获得奖学金(处理组),<60分的学生为控制组,使用rdrobust命令进行估计时,设定c(60)表示阈值为60分,bwselect(0.8)表示选择最优带宽为0.8(即选取阈值前后0.8个标准差的样本),kernel(epan)表示使用Epanechnikov核函数,估计结果显示,奖学金政策使学生平均成绩提高了5.2分(p<0.05),表明政策具有显著的正向效果,进一步通过rdplot绘制散点图,可见60分两侧的成绩拟合曲线出现明显断点,且左侧样本分布无明显堆积,支持断点回归的有效性。

相关问答FAQs:
-
问:断点回归命令与双重差分法(DID)的主要区别是什么?
答:断点回归命令(RDD)依赖于“ running variable ”在阈值附近的局部随机性,通过比较阈值两侧的样本差异估计处理效应,适用于存在明确分界线的场景;而双重差分法(DID)通过比较处理组和控制组在政策前后的差异变化,控制时间趋势和组间差异,适用于政策实施前后的面板数据,RDD的优势在于内部有效性较强,但外部有效性可能受限;DID则依赖于平行趋势假设,若政策外生性不满足,估计结果可能存在偏差。 -
问:如何判断断点回归分析中是否存在“ running variable ”的操纵现象?
答:检验“ running variable ”的操纵现象是断点回归有效性的关键步骤,常用的方法包括:绘制“ running variable ”在阈值附近的直方图或核密度图,观察阈值两侧的样本分布是否对称;进行McCrary检验,通过比较阈值两侧的密度函数是否连续,若密度函数在阈值处出现显著跳跃,则可能存在操纵现象,还可以检验“ running variable ”与个体特征(如年龄、性别)在阈值两侧的分布是否连续,若存在显著差异,则表明样本可能存在选择性偏差。