要证明菱形的四个顶点共圆,需要从菱形的性质出发,结合圆的定义及相关几何定理进行推导,菱形是一种特殊的平行四边形,其四条边长度相等,对角线互相垂直平分且平分一组对角,这些性质为证明四点共圆提供了重要依据,以下是详细的证明过程及相关分析。

菱形的基本性质
回顾菱形的定义及性质:
- 四条边相等:菱形的四条边长度相同,即 ( AB = BC = CD = DA )。
- 对角线互相垂直平分:对角线 ( AC ) 和 ( BD ) 相交于点 ( O ),且 ( AC \perp BD ),( AO = OC ),( BO = OD )。
- 对角相等:菱形的对角相等,即 ( \angle ABC = \angle ADC ),( \angle BAD = \angle BCD )。
- 邻角互补:菱形的邻角之和为 ( 180^\circ ),即 ( \angle ABC + \angle BAD = 180^\circ )。
四点共圆的判定方法
四点共圆是指四个点位于同一个圆上,常用的判定方法包括:
- 对角互补:如果一个四边形的对角互补,则其四个顶点共圆。
- 同底等角:如果两个点在同一条线段的同侧,且对该线段的张角相等,则这两个点与线段的端点共圆。
- 垂直平分线法:如果四个点到某一定点的距离相等,则这四点共圆。
证明菱形四点共圆的具体步骤
利用对角互补的性质
根据菱形的性质,邻角互补,即 ( \angle ABC + \angle BAD = 180^\circ ),根据四点共圆的判定定理,如果一个四边形的对角互补,则其四个顶点共圆,菱形的四个顶点 ( A )、( B )、( C )、( D ) 共圆。
利用对角线的性质
菱形的对角线互相垂直平分,设对角线 ( AC ) 和 ( BD ) 相交于点 ( O ),由于 ( AO = OC ),( BO = OD ),且 ( AC \perp BD ),可以证明 ( O ) 是菱形的外接圆圆心,具体步骤如下:
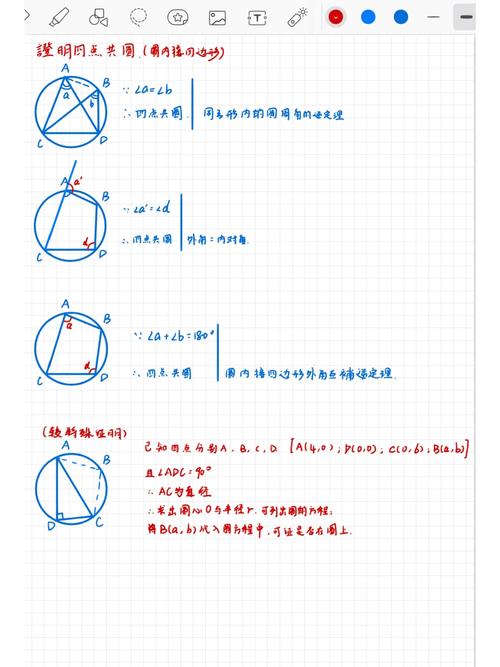
- 连接 ( OA )、( OB )、( OC )、( OD )。
- 由于 ( AO = OC ),( BO = OD ),且 ( \angle AOB = \angle BOC = \angle COD = \angle DOA = 90^\circ )(因为对角线垂直)。
- 根据勾股定理,( OA = OB = OC = OD ),即四个顶点到点 ( O ) 的距离相等。
- 点 ( A )、( B )、( C )、( D ) 都以 ( O ) 为圆心,( OA ) 为半径的圆上,四点共圆。
利用等腰三角形的性质
菱形的四条边相等,( \triangle ABD ) 和 ( \triangle CBD ) 都是等腰三角形,设 ( AC ) 和 ( BD ) 相交于 ( O ),则 ( \triangle AOB )、( \triangle BOC )、( \triangle COD )、( \triangle DOA ) 都是等腰直角三角形,通过计算这些三角形的边长和角度,可以证明四个顶点到 ( O ) 的距离相等,从而四点共圆。
验证与总结
为了验证上述证明的正确性,可以通过具体数值计算或几何作图进行验证,设菱形的边长为 ( a ),对角线 ( AC = 2p ),( BD = 2q ),则根据菱形的性质,( p^2 + q^2 = a^2 ),由于 ( OA = p ),( OB = q ),且 ( \angle AOB = 90^\circ ),则 ( OA = OB = OC = OD ),进一步确认四点共圆。
相关问答FAQs
问题1:菱形和矩形的四个顶点是否都共圆?为什么?
解答:菱形的四个顶点共圆,但矩形的四个顶点不一定共圆,菱形的对角线互相垂直平分,且四条边相等,因此其对角互补或对角线交点到各顶点的距离相等,满足四点共圆的条件,而矩形虽然对角线相等且互相平分,但只有当矩形是正方形时(即对角线垂直),四个顶点才共圆;一般的矩形对角线不垂直,因此四个顶点不共圆。
问题2:如何判断一个四边形的四个顶点是否共圆?
解答:判断四点共圆的方法有多种,包括:
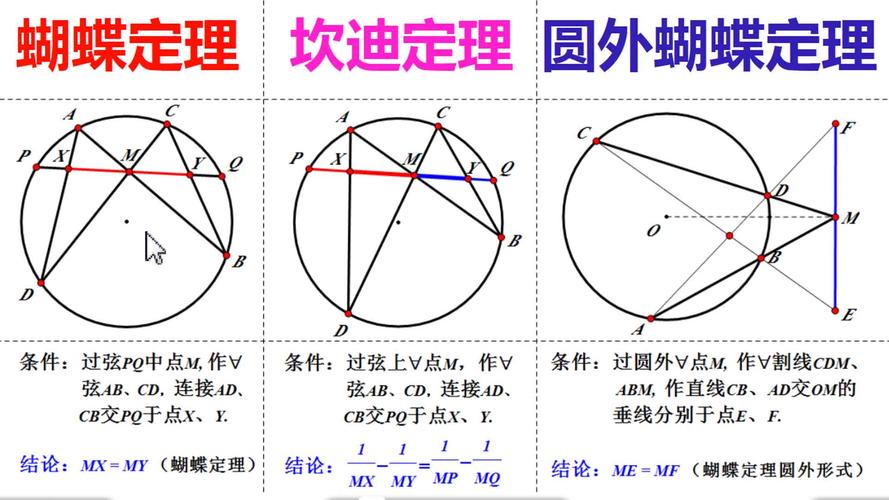
- 对角互补法:如果四边形的对角互补(即 ( \angle A + \angle C = 180^\circ ),( \angle B + \angle D = 180^\circ )),则四点共圆。
- 同底等角法:如果两个点在同一条线段的同侧,且对该线段的张角相等(即 ( \angle APB = \angle AQB )),则 ( A )、( B )、( P )、( Q ) 四点共圆。
- 距离相等法:如果四个点到某一定点的距离相等,则这四点共圆。
- 圆周角定理:如果一条线段的两端点对另外两个点的张角相等,则这四点共圆。
通过以上方法,可以系统地判断任意四边形的四个顶点是否共圆。