要找到阿波罗尼斯圆的圆心,首先需要明确阿波罗尼斯圆的定义及其几何性质，阿波罗尼斯圆是指平面上到两个定点（称为基点）的距离之比为常数（不等于1）的点的轨迹，设这两个基点为A和B，距离比为k（k>0且k≠1），则满足PA/PB=k的点P的轨迹就是一个圆，这个圆被称为阿波罗尼斯圆，其圆心的位置与基点A、B的坐标以及比例k密切相关，以下通过代数法和几何法详细说明求解过程。
代数法求解圆心坐标
代数法是通过建立坐标系,利用距离公式和比例条件推导圆心坐标，具体步骤如下：
-
设定坐标系与基点坐标
设基点A的坐标为(x₁, y₁)，基点B的坐标为(x₂, y₂)，为简化计算，可先将坐标系进行平移和旋转，使基点A位于原点(0,0)，基点B位于x轴正半轴上的(c,0)，其中c=|AB|为两基点之间的距离，这一步可通过坐标变换实现，变换后的圆心坐标再通过逆变换还原到原坐标系。 -
建立距离比例方程
设动点P的坐标为(x,y)，根据阿波罗尼斯圆的定义，有PA/PB=k，即：
[ \frac{\sqrt{x^2 + y^2}}{\sqrt{(x - c)^2 + y^2}} = k ]
两边平方后整理得：
[ x^2 + y^2 = k^2 \left[(x - c)^2 + y^2\right] ]
展开并化简：
[ x^2 + y^2 = k^2(x^2 - 2cx + c^2 + y^2) ]
[ (1 - k^2)x^2 + (1 - k^2)y^2 + 2k^2cx - k^2c^2 = 0 ]
由于k≠1，可两边除以(1 - k²)，得到圆的方程标准形式：
[ x^2 + y^2 + \frac{2k^2c}{1 - k^2}x - \frac{k^2c^2}{1 - k^2} = 0 ] -
确定圆心与半径
将上述方程整理为圆的标准方程(x - a)² + (y - b)² = r²，通过配方可得圆心坐标(a,b)，对x项配方：
[ x^2 + \frac{2k^2c}{1 - k^2}x = \left(x + \frac{k^2c}{1 - k^2}\right)^2 - \left(\frac{k^2c}{1 - k^2}\right)^2 ]
圆心在x轴上的坐标为：
[ a = -\frac{k^2c}{1 - k^2} = \frac{k^2c}{k^2 - 1} ]
y坐标b=0（因方程中无y的一次项），圆心坐标为(\left(\frac{k^2c}{k^2 - 1}, 0\right))。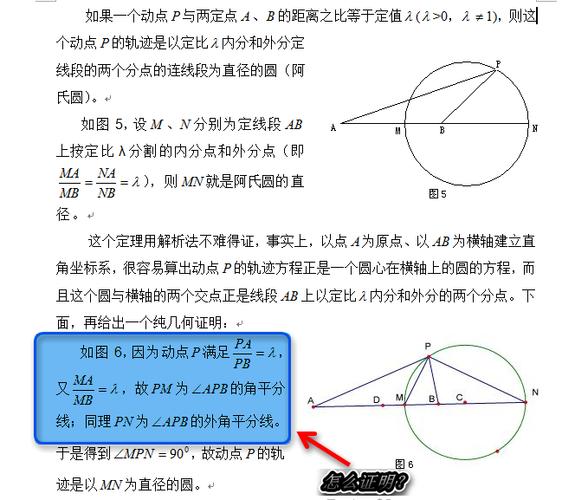
（图片来源网络，侵删）若基点A、B不在简化坐标系中，设原坐标系中A(x₁,y₁)、B(x₂,y₂)，则圆心坐标可通过向量计算：
[ \text{圆心} = \left(\frac{k^2x_2 - x_1}{k^2 - 1}, \frac{k^2y_2 - y_1}{k^2 - 1}\right) ]
该公式是通过将简化坐标系中的圆心坐标通过逆平移和旋转得到的，适用于任意位置的基点。
几何法求解圆心位置
几何法利用阿波罗尼斯圆的几何性质直接定位圆心,无需复杂计算，核心性质包括：
-
圆心在基点连线上
阿波罗尼斯圆的圆心始终位于两个基点A、B的连线上，这是因为距离比例条件PA/PB=k具有对称性，圆心作为轨迹的对称中心，必然在AB直线上。 -
内外分点的定义
在AB连线上存在两个特殊点：内分点C和外分点D，它们将AB分为比例k，具体而言：
（图片来源网络，侵删）- 内分点C满足AC/CB=k，且C在A、B之间，坐标为：
[ C = \left(\frac{kx_2 + x_1}{k + 1}, \frac{ky_2 + y_1}{k + 1}\right) ] - 外分点D满足AD/DB=k，且D在AB的延长线上，坐标为：
[ D = \left(\frac{kx_2 - x_1}{k - 1}, \frac{ky_2 - y_1}{k - 1}\right) ]
阿波罗尼斯圆的圆心O即为CD的中点，因此圆心坐标为C和D坐标的平均值：
[ O = \left(\frac{C_x + D_x}{2}, \frac{C_y + D_y}{2}\right) = \left(\frac{k^2x_2 - x_1}{k^2 - 1}, \frac{k^2y_2 - y_1}{k^2 - 1}\right) ]
这与代数法得到的结果一致。
- 内分点C满足AC/CB=k，且C在A、B之间，坐标为：
-
半径的确定
阿波罗尼斯圆的半径可以通过圆心O到点C或D的距离计算，半径r=|OC|=|OD|，具体表达式为：
[ r = \frac{k \cdot |AB|}{|k^2 - 1|} ]
AB|为两基点之间的距离。
具体计算步骤示例
假设基点A(0,0)、B(4,0)，比例k=2，求解阿波罗尼斯圆的圆心。
-
代数法计算
代入圆心公式：
[ O = \left(\frac{2^2 \cdot 4 - 0}{2^2 - 1}, \frac{2^2 \cdot 0 - 0}{2^2 - 1}\right) = \left(\frac{16}{3}, 0\right) ]
半径r= (\frac{2 \cdot 4}{|4 - 1|} = \frac{8}{3})。 -
几何法验证
- 内分点C：(\left(\frac{2 \cdot 4 + 0}{2 + 1}, 0\right) = \left(\frac{8}{3}, 0\right))
- 外分点D：(\left(\frac{2 \cdot 4 - 0}{2 - 1}, 0\right) = (8, 0))
- 圆心O为CD中点：(\left(\frac{\frac{8}{3} + 8}{2}, 0\right) = \left(\frac{16}{3}, 0\right))，与代数法一致。
特殊情况与注意事项
-
k=1时的退化情况
当k=1时，轨迹变为AB的垂直平分线（一条直线），而非圆，因此阿波罗尼斯圆的定义中k≠1。 -
坐标系的选择
为简化计算，建议将基点置于坐标轴上，但最终结果需通过坐标变换还原到原坐标系，若基点坐标复杂，可直接使用通用公式计算。 -
比例k的取值范围
k>0且k≠1，k的值影响圆心的位置：当k>1时，圆心靠近B点；当0<k<1时，圆心靠近A点。
阿波罗尼斯圆的圆心可通过代数法（距离公式推导）或几何法（内外分点中点）确定，核心在于利用距离比例条件建立方程或利用几何性质定位，圆心坐标公式为(\left(\frac{k^2x_2 - x_1}{k^2 - 1}, \frac{k^2y_2 - y_1}{k^2 - 1}\right))，适用于任意基点A(x₁,y₁)、B(x₂,y₂)和比例k(k>0,k≠1)，实际应用中，可根据坐标系复杂度选择代数法或几何法，注意k=1时的退化情况。
相关问答FAQs
问题1：阿波罗尼斯圆的圆心是否一定在两个基点的连线上？
解答：是的，阿波罗尼斯圆的圆心必然位于两个基点A、B的连线上，这是因为距离比例PA/PB=k具有轴对称性，圆心作为轨迹的对称中心，必须在AB直线上，这一性质是几何法求解圆心位置的基础，也是区分阿波罗尼斯圆与其他圆的重要特征。
问题2：如果两个基点的坐标不是简单的(0,0)和(c,0)，如何快速计算圆心？
解答：可直接使用通用公式计算，设基点A(x₁,y₁)、B(x₂,y₂)，比例k(k≠1)，圆心坐标为(\left(\frac{k^2x_2 - x_1}{k^2 - 1}, \frac{k^2y_2 - y_1}{k^2 - 1}\right))，该公式通过坐标系变换和代数推导得到，适用于任意位置的基点，无需手动进行平移或旋转操作，可直接代入坐标计算，A(1,2)、B(5,6)、k=3时，圆心为(\left(\frac{9 \cdot 5 - 1}{9 - 1}, \frac{9 \cdot 6 - 2}{9 - 1}\right) = \left(\frac{44}{8}, \frac{52}{8}\right) = (5.5, 6.5))。
