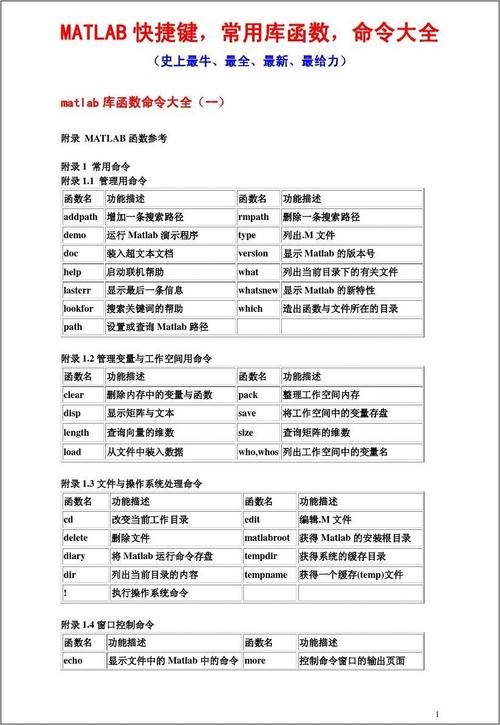
在MATLAB中,计算命令是进行数值运算、符号计算和数据分析的核心工具,涵盖了从基础算术运算到复杂矩阵操作、函数求解等多个方面,以下将详细介绍常用的MATLAB计算命令及其应用场景。
基础算术运算命令包括加()、减()、乘()、除()和乘方(^),这些操作符可直接用于标量、向量或矩阵。a=2; b=3; c=a+b会计算a与b的和并赋值给c,对于矩阵运算,MATLAB区分点乘()、点除()和点乘方(.^),这些操作符会对矩阵的对应元素逐个进行运算,而、等则执行矩阵整体的线性代数运算。sum函数用于求和(如sum(A)计算矩阵A所有元素的和),mean计算平均值,max和min分别求最大值和最小值,sqrt计算平方根,exp计算自然指数,log计算自然对数,sin、cos、tan等则是三角函数命令。
矩阵运算命令是MATLAB的强项。zeros(m,n)生成m×n的零矩阵,ones(m,n)生成全1矩阵,eye(n)生成n×n单位矩阵,rand(m,n)生成均匀分布的随机矩阵,randn(m,n)生成标准正态分布的随机矩阵,矩阵转置用(如A'),逆矩阵通过inv(A)计算,行列式用det(A),矩阵的秩由rank(A)得到,对于线性方程组Ax=b,x=A\b是最小二乘解,而x=inv(A)*b虽然也能求解,但前者在数值上更稳定。
数值计算方面,fzero用于求解一元方程的根(如fzero(@(x)x^2-4,1)从初始值1开始求解x^2-4=0),fsolve可求解非线性方程组(需定义函数句柄和初始值),积分运算中,integral用于数值积分(如integral(@(x)exp(-x.^2),0,inf)计算高斯积分),trapz则采用梯形法求积,微分方程求解可通过ode45实现(如[t,y]=ode45(@(t,y)-y,0,1,[1])求解dy/dt=-y)。
符号计算需借助Symbolic Math Toolbox,通过syms定义符号变量(如syms x y),然后使用solve解方程(如solve(x^2+2*x-1==0,x)),diff求导(如diff(sin(x),2)求二阶导数),int求积分(如int(x^2,x,0,1)),limit计算极限(如limit(sin(x)/x,x,0))。

以下是部分常用计算命令的总结:
| 功能类别 | 命令示例 | 说明 |
|---|---|---|
| 矩阵生成 | A = [1,2;3,4] |
创建2×2矩阵 |
| 元素运算 | B = A .* 2 |
矩阵A每个元素乘以2 |
| 矩阵逆 | C = inv(A) |
求矩阵A的逆 |
| 方程求解 | x = A \ b |
解线性方程组Ax=b |
| 数值积分 | Q = integral(@(x)x.^2,0,1) |
计算x^2在[0,1]的积分 |
| 符号求导 | dydx = diff(x^2,x) |
求x^2的一阶导数 |
相关问答FAQs
Q1: MATLAB中如何计算矩阵的特征值和特征向量?
A1: 使用eig函数。A = [1,2;3,4]; [V,D] = eig(A)会返回特征向量矩阵V和特征值对角矩阵D;若仅需特征值,可用e = eig(A)。
Q2: 如何在MATLAB中实现自定义函数的数值积分?
A2: 首先通过定义匿名函数,如f = @(x) sin(x).*x;,然后调用integral函数,如result = integral(f,0,pi),计算sin(x)*x在[0,π]上的定积分。