认识“角”的基本结构
所有类型的角都由两条射线(称为“边”)和一个共同的端点(称为“顶点”)组成,打开书本时书脊的位置就是顶点,两页纸的边缘则是两条边,可以用手势模拟:伸出食指和中指形成“V”字形,指尖交汇处即为顶点,两根手指代表两条边。

✅ 关键特征归纳表
| 组成部分 | 定义 | 示例 |
|---|---|---|
| 顶点 | 两条边的交点 | 钟表指针的中心点 |
| 边 | 从顶点出发的直直的线 | 三角尺的斜面边缘 |
| 开口方向 | 决定角的大小与类型 | 门缝开合的角度变化 |
区分不同类型的角——按度数划分
通过量角器测量后,可根据角度范围将角分为以下几类(建议配合实物道具演示):
-
锐角(<90°)
- 特点:比直角小,看起来“尖尖的”。
✔️ 例:等腰三角形顶角、切片披萨的每一块尖端。
✖️ 易错点:不要误以为细长的图形才是锐角,关键在于度数而非形状长短。
- 特点:比直角小,看起来“尖尖的”。
-
直角(=90°)
- 检验方法:用三角板的直角边框完全贴合被测角,若两边重合则确认为直角,生活中常见于方桌角落、纸张边缘交接处。
💡记忆口诀:“方方正正九十度。”
- 检验方法:用三角板的直角边框完全贴合被测角,若两边重合则确认为直角,生活中常见于方桌角落、纸张边缘交接处。
-
钝角(>90°且<180°)
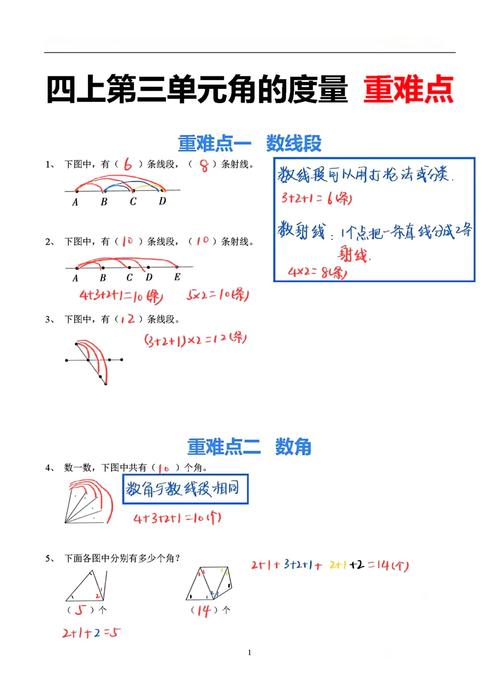 (图片来源网络,侵删)
(图片来源网络,侵删)- 对比法:明显大于直角但未达到平角的状态,如衣架挂勾张开的角度、半开的折扇,可用A4纸对折两次形成近似钝角辅助理解。
-
平角(=180°)
- 动态演示:将两根小棒一端固定作为顶点,旋转其中一根至与另一根成直线反向延伸,此时形成的即是平角,注意它看似一条直线实则由两个相反方向的射线构成。
-
周角(=360°)
- 生活实例:旋转木马转一圈回到原位所形成的轨迹就是周角,可用圆规画圆的过程帮助学生可视化这一概念。
🔍 度数区间速查表
| 类型 | 度数范围 | 典型场景举例 |
|---|---|---|
| 锐角 | 0°~89° | 剪刀闭合时的最小夹角 |
| 直角 | 恰好90° | 黑板擦角落、魔方每个面的拐角 |
| 钝角 | 91°~179° | 电脑屏幕展开支架的角度 |
| 平角 | 正好180° | 体操运动员劈叉姿势的身体线 |
| 周角 | 完整360° | 时钟指针绕表盘一圈 |
实用辨别技巧大公开
▶︎ 肉眼初判三步法
- 找顶点 → 确定角的中心位置;
- 估张口 → 根据开口宽度初步猜测类型(窄→锐/宽→钝);
- 比参照物 → 联想已知角度物体进行对照(如课本封面是矩形含四个直角)。
▶︎ 工具精准验证法
正确使用量角器的操作流程:
① 中心对准顶点;② 零刻度线与任意一边重合;③ 读取另一条边对应的刻度值,特别强调内外圈刻度的区分原则:当被测边落在右侧时读内圈数值,左侧则读外圈数值。
▶︎ 特殊标记识别术
在几何图中,常用弧线标注不同类别的角:单个弧线多为锐角或钝角,加小方块表示直角,而平角通常用直线加箭头符号示意其延展性,教师可在黑板上绘制范例并让学生临摹练习。
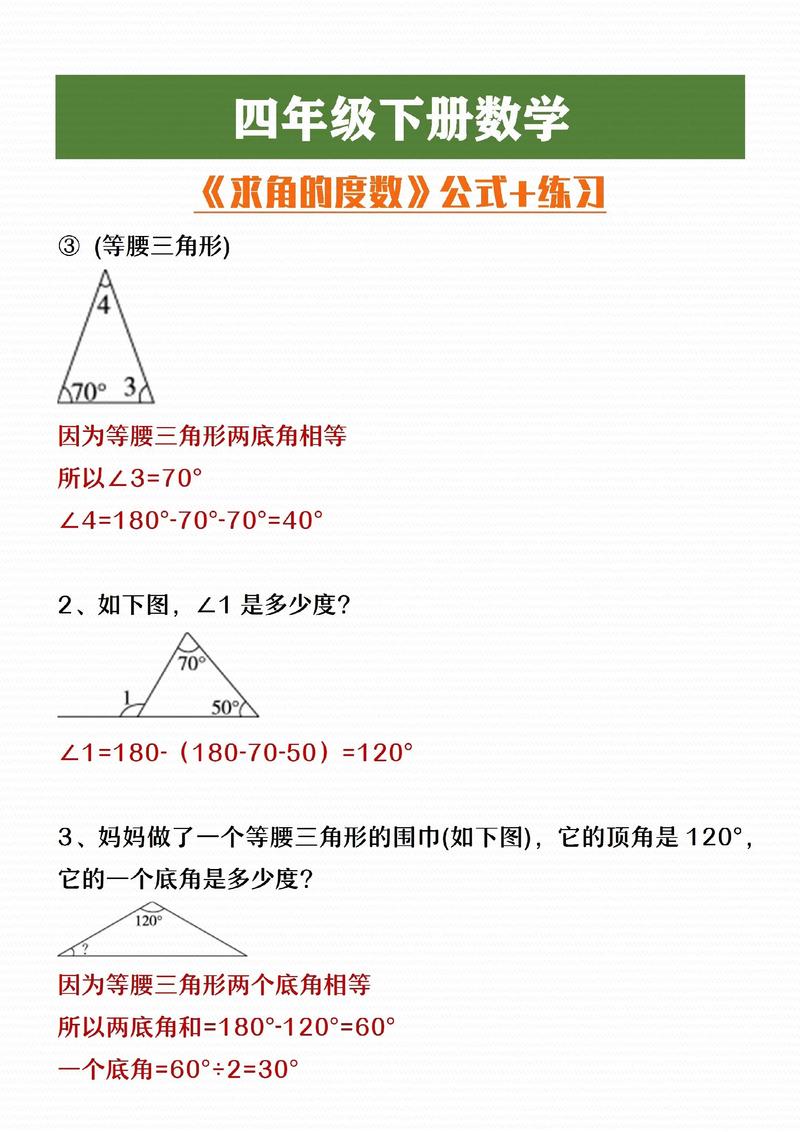
常见误区警示栏
⚠️ 错误观念纠正清单
- × “长得大的图形里面的角一定更大”——实际需用量角器验证,视觉可能有偏差;
- × “只要是尖的就是锐角”——必须严格按度数判断,有些钝角也可能显得较纤细;
- × “所有的钝角都比锐角有用”——各类角在不同场景下均有重要作用,无优劣之分。
课堂互动实践活动推荐
设计分层任务促进深度理解:
🔹 基础组:用吸管搭建不同种类的角并贴上标签;
🔹 进阶组:在校园内寻找五个以上的自然形成的角并记录其类型;
🔹 挑战组:合作创作一幅包含所有五种角的艺术画,要求标注名称及大致度数。
FAQs(常见问题解答)
Q1:为什么同一个角有人觉得是锐角而另一个人认为是钝角?
答:这是因为每个人的视觉估算存在差异,尤其在接近临界值(如89°vs91°)时容易产生分歧,唯一可靠的方式是使用量角器进行精确测量,避免主观判断误差。
Q2:是否存在既是锐角又是钝角的情况?
答:绝对不可能,根据定义,一个角只能属于某一特定类别,若出现矛盾上文归纳,必然是由于测量错误或读数失误导致,需要重新检查操作步骤是否正确


