AI绘制圆角多边形的过程融合了几何计算、图形渲染算法和用户交互设计,其核心在于通过数学模型控制多边形的顶点位置与圆角半径,确保图形既符合几何规则又具备视觉美感,以下是详细的技术实现路径和应用场景分析。
圆角多边形的数学基础
圆角多边形本质是直线段与圆弧的平滑连接组合,传统多边形由顶点和直线边构成,而圆角多边形需在每个顶点处替换为圆弧,其数学定义包含三个关键参数:顶点坐标(x_i, y_i)、边长(L_i)和圆角半径(r),圆角半径需满足约束条件:r ≤ min(Li, L{i+1})/2,否则相邻圆弧会重叠导致图形变形。
以六边形为例,设中心坐标为(cx, cy),外接圆半径为R,顶点坐标可通过极坐标计算:(cx + R·cos(θ_i), cy + R·sin(θ_i)),_i = i·π/3(i=0,1...5),圆角处理时,需计算每个顶点处的两条相邻边的单位向量ui和u{i+1},通过向量旋转得到圆弧的起点和终点坐标,圆弧的圆心位于顶点沿角平分线方向移动r·(1/cos(α/2))的位置,为内角。
AI实现的技术路径
参数化建模法
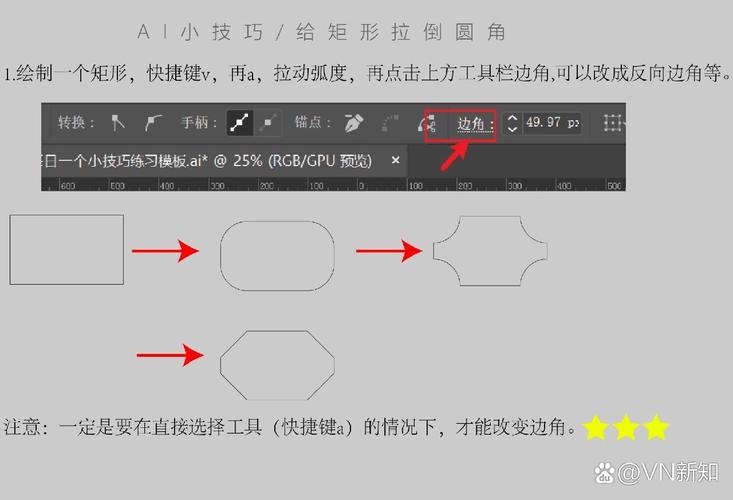
通过参数方程直接生成圆角多边形顶点,以矩形为例,给定长宽(a,b)和圆角半径r,四个顶点坐标为(r,r)、(a-r,r)、(a-r,b-r)、(r,b-r),圆弧部分使用贝塞尔曲线逼近,这种方法适用于规则图形,计算效率高,但灵活性有限。
离散化逼近法
对于不规则多边形,采用“直线段+圆弧”分段处理,首先计算原始多边形的顶点序列,然后对每个顶点执行以下步骤:

- 计算相邻边的单位向量u1, u2
- 求解角平分线方向向量n = (u1 + u2)/|u1 + u2|
- 计算圆弧起点P1 = 顶点 + r·u1,终点P2 = 顶点 + r·u2
- 圆弧圆心C = 顶点 + r·n / cos(θ/2),θ为两边的夹角
- 使用三次贝塞尔曲线模拟圆弧,控制点设为C ± r·sin(θ/2)·n⊥
机器学习优化法
针对复杂图形生成,可采用生成对抗网络(GAN)或变分自编码器(VAE)学习圆角多边形的分布特征,训练数据包含大量手动设计的圆角多边形及其参数(顶点数、半径比例、曲率变化等),通过对抗训练使AI生成符合美学规律的图形,StyleGAN模型可通过噪声向量控制圆角的自然过渡,避免机械感。
实时渲染技术
在图形处理单元(GPU)中,可通过片段着色器实现动态圆角效果,将多边形视为多个扇形区域的组合,在顶点着色器中传递圆角半径信息,片段着色器根据像素到顶点的距离判断是否绘制圆弧,这种方法支持实时交互调整,适用于UI设计工具。
不同工具的实现差异
| 工具类型 | 代表软件 | 核心技术 | 优势 | 局限性 |
|---|---|---|---|---|
| 向量设计软件 | Adobe Illustrator | 贝塞尔曲线控制点算法 | 精确编辑,支持矢量输出 | 复杂图形计算量大 |
| 3D建模软件 | Blender | 离散化+曲面细分 | 支持立体化渲染 | 参数调整不够直观 |
| 编程库 | Python Matplotlib | 参数方程+抗锯齿渲染 | 高度定制化,适合批量生成 | 需编程基础 |
| AI设计平台 | Midjourney | 扩散模型+美学约束 | 快速创意生成 | 难以精确控制几何参数 |
应用场景与优化方向
在UI设计中,圆角多边形常用于按钮、图标等元素,AI可通过学习Material Design或Human Interface Design规范自动生成符合平台规范的图形,在工业设计领域,AI可根据力学需求优化圆角半径分布,例如在应力集中区域增大圆角以减少裂纹风险。
当前技术挑战包括:自相交多边形的圆角处理、非均匀圆角的平滑过渡、以及高维空间(如3D曲面)上的圆角多边形生成,未来研究方向可能集中在基于物理的渲染(PBR)与圆角多边形的结合,以及通过强化学习实现用户偏好驱动的自动优化。

相关问答FAQs
Q1: AI生成的圆角多边形如何确保与设计规范的一致性?
A1: 可通过约束优化算法实现,首先将设计规范(如最小圆角半径、最大边长比)转化为数学不等式,然后使用拉格朗日乘数法或遗传算法在生成过程中实时约束参数,在UI设计中,可将平台规范编码为惩罚函数,当AI生成的图形违反规范时增加损失值,通过梯度下降引导模型向符合规范的方向优化。
Q2: 如何解决圆角多边形在缩放时的变形问题?
A2: 采用自适应半径算法,根据图形缩放比例动态调整圆角半径r,保持r与边长的比例恒定,具体实现需记录原始图形的r/L比值(L为边长),缩放时按新边长L' = k·L重新计算r' = r·k,对于非均匀缩放,可分别计算x和y方向的缩放因子,取较大值作为r的调整基准,确保视觉协调性,在矢量图形中,还可通过贝塞尔曲线的控制点缩放实现更自然的变形效果。