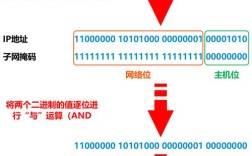
在解决成比例问题时,设未知数是关键步骤,合理的未知数设定能简化计算过程并清晰反映数量关系,成比例问题通常涉及两种相关联的量,它们之间存在正比例或反比例关系,通过设定未知数可以将文字关系转化为数学方程,进而求解未知量,以下是设未知数的具体方法和注意事项。

需明确题目中的比例关系,若两种量成正比例(即比值一定),如速度一定时路程与时间的关系,可设其中一个量为未知数,另一个量用含未知数的式子表示,已知汽车行驶速度为60 km/h,设行驶时间为t小时,则路程s=60t,若题目中给出具体数值对应关系,如“3小时行驶180 km”,可先求出比值(180÷3=60),再设未知数,若问题涉及多个量,需根据比例性质统一设未知数,若a∶b=2∶3,b∶c=4∶5,可设b为12(3和4的最小公倍数),则a=8,c=15,从而建立各量之间的关系。
对于反比例问题(即乘积一定),如工作总量一定时工作效率与工作时间的关系,需设未知数后表达乘积关系,完成一项工作,甲单独做需5天,乙单独做需x天,若两人合作效率为(1/5+1/x),合作时间为t天,则可列方程(1/5+1/x)t=1,此时需注意未知数的实际意义,避免出现不合逻辑的解。
在涉及多个比例的复合问题中,可采用“单位量法”设未知数,已知甲、乙、丙三人钱数之比为3∶4∶5,总钱数为360元,可设一份为x元,则甲为3x,乙为4x,丙为5x,列方程3x+4x+5x=360,解得x=40,进而求出各量,这种方法适用于比例关系明确且总量已知的情况。
中给出比例变化后的结果,可通过“不变量”设未知数,原来男生与女生人数之比为5∶3,后来男生增加10人,女生减少5人,比例变为5∶4,此时可设原来男生为5x,女生为3x,根据男生人数不变(或女生人数不变)列方程,但需注意本题中男生人数变化,需根据比例变化后的关系列方程:(5x+10)∶(3x-5)=5∶4,解得x=15。
以下是设未知数的常见类型及示例表格:

| 问题类型 | 设未知数方法 | 示例 |
|---|---|---|
| 正比例问题 | 设单一量为x,另一量用比例表示 | 速度一定,时间t与路程s成正比,s=60t |
| 反比例问题 | 设未知数表达乘积关系 | 工作总量一定,效率p与时间t成反比,p·t=W(常数) |
| 多比例复合问题 | 设“一份”为x | a∶b∶c=2∶3∶4,设a=2x,b=3x,c=4x |
| 比例变化问题 | 找不变量设未知数 | 原比例a∶b=3∶2,a增加6后比例变为5∶4,设原a=3x,b=2x,列(3x+6)∶2x=5∶4 |
设未知数时需注意:1)未知数的个数应尽量少,简化计算;2)根据实际问题选择设直接未知数或间接未知数;3)检查解的合理性,如人数、时间等需为正数。
相关问答FAQs
Q1:在成比例问题中,如何选择设直接未知数还是间接未知数?
A1:若问题所求量即为未知数,且能直接与其他量建立比例关系,可设直接未知数,如“求某量x,根据x∶y=m∶n”直接设x,若直接设未知数会导致方程复杂,或需通过中间量求解,则设间接未知数,已知比例a∶b=2∶3,且a+b=10,可设a=2x,b=3x(间接),比直接设a为x更简便。
Q2:比例问题中,若比例值不是整数,如何设未知数更简便?
A2:可将比例值化为整数后再设未知数,比例a∶b=1.5∶2,可两边同乘2得3∶4,再设a=3x,b=4x,避免小数计算,若比例值为分数,如a∶b=2/3∶1/4,可同乘12得8∶3,设a=8x,b=3x,简化运算。