在数学学习和实际测量中,精确测量长度是一项基础且重要的技能,以测量3厘米为例,这一看似简单的任务需要结合正确的工具、规范的步骤和数学思维的运用,以下将从工具选择、操作步骤、误差分析、数学应用延伸及常见误区等多个维度,详细阐述如何准确测量3厘米,并融入“张嘴”这一拟人化表达,强调测量过程中需保持“张嘴”状态的严谨与细致——即观察清晰、操作规范、数据准确。
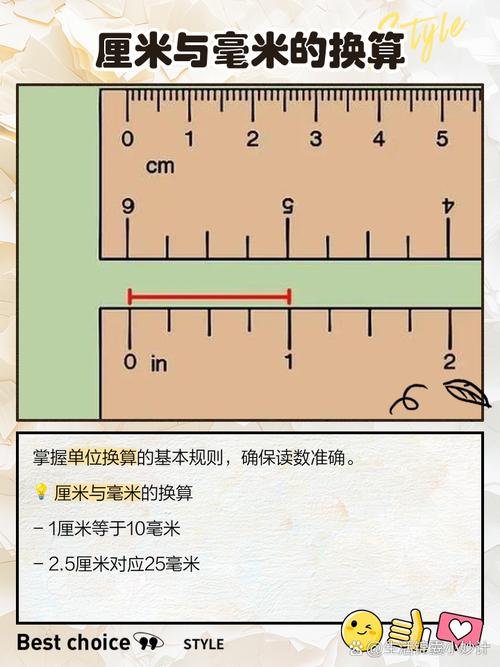
测量工具的选择与准备
测量3厘米的长度,需根据精度要求选择合适的工具,常用工具包括直尺、三角尺、游标卡尺(高精度场景)等,对于日常学习和基础测量,透明塑料直尺是首选,其刻度清晰、便于读数,选择工具时需注意:
- 刻度完整性:确保直尺的“0”刻线清晰完整,无磨损或模糊。
- 最小刻度值:直尺的最小刻度通常为1毫米,满足3厘米(30毫米)的测量需求;若需更高精度,可选用游标卡尺(最小刻度0.02毫米)。
- 工具状态:检查直尺是否平直,避免因弯曲导致测量误差。
准备阶段需将待测物体(如纸条、文具等)放置在水平桌面上,确保物体无折叠、无卷曲,与测量基准面完全贴合。
规范测量步骤
测量3厘米的核心是“对准零刻度、保持水平、视线垂直”,具体操作如下:
确定测量起点
将直尺的“0”刻度线与待测物体的一端对齐,此处需注意“对齐”的细节:若物体边缘较薄(如纸张),应使“0”刻度线与物体边缘完全重合;若物体有厚度(如木块),需以物体一侧的端面为基准,避免刻度线与端面间出现空隙。

固定直尺与物体
用左手手指轻按直尺,防止滑动;右手调整物体位置,确保物体另一端与直尺刻度线平行,此时需“张嘴”观察——即眼睛俯视直尺,确认物体与直尺刻度线之间无间隙、无倾斜。
读取终点刻度
移动视线至物体另一端,使视线与直尺刻度线垂直(避免视差误差),找到与物体端点对齐的刻度线,若端点位于两条刻度线之间,需估读。
- 若端点对齐“3”刻度线(即30毫米),则测量结果为3厘米;
- 若端点位于“3”与“4”刻度线中间,可估读为3.5厘米(35毫米),但3厘米的测量通常无需估读,只需精确到最小刻度。
记录与重复测量
记录数据后,可重复测量2-3次,取平均值以减少随机误差,三次测量结果分别为2.98厘米、3.02厘米、3.00厘米,则平均值为3.00厘米。
误差分析与控制
测量误差不可避免,但可通过规范操作将其降至最低:

| 误差类型 | 产生原因 | 控制方法 |
|---|---|---|
| 系统误差 | 直尺刻度不准(如“0”刻线磨损) | 选择合格工具,定期校准 |
| 视差误差 | 视线与刻度线不垂直 | 保持“张嘴”状态,视线垂直于刻度面 |
| 操作误差 | 直尺倾斜或物体未贴合 | 用三角板辅助直尺保持水平,确保物体无翘曲 |
| 估读误差 | 最小刻度以下的估读偏差 | 3厘米测量无需估读,直接读取整数刻度 |
若直尺“0”刻线磨损后实际从1毫米处开始,测量结果将偏小1毫米,需修正读数。
数学思维的延伸应用
测量不仅是操作技能,更是数学思维的实践:
- 单位换算:3厘米=30毫米=0.03米=0.03×100=3%(以1米为单位1的百分比表达)。
- 比例关系:若地图比例尺为1:100,则3厘米的图上距离代表实际3×100=300厘米=3米。
- 几何应用:测量长方形纸条的长为3厘米,宽为2厘米,可计算面积(3×2=6平方厘米)和周长(2×(3+2)=10厘米)。
通过测量,将抽象的“厘米”与具体物体关联,深化对“量”的理解。
常见误区与注意事项
- 误区一:认为“3厘米”必须精确对齐刻度线,忽略物体端点与刻度线的对齐方式。
纠正:以物体端面为基准,而非刻度线本身。 - 误区二:测量时直尺一端悬空,导致直尺弯曲变形。
纠正:用直尺的整个底部支撑物体,避免悬空。 - 误区三:多次测量结果差异大却忽略环境因素(如温度导致热胀冷缩)。
纠正:在稳定环境下测量,对精密工具需考虑温度修正。
相关问答FAQs
Q1: 为什么用直尺测量时,视线必须垂直于刻度线?
A: 若视线倾斜(如从左侧或右侧俯视),会导致“视差误差”,当物体端点对齐“3”刻度线时,斜视可能误读为“2.9”或“3.1”厘米,垂直视线可确保读数与实际刻度重合,保证准确性。
Q2: 如果直尺的最小刻度是1厘米,如何测量3厘米?
A: 若直尺最小刻度为1厘米(部分教学用直尺),可直接读取“3”刻度线对应的数值,但需注意此类直尺精度较低,仅适用于对精度要求不高的场景,若需更精确结果,应换用最小刻度为1毫米的直尺,避免因刻度间隔过大导致估读困难。