在计算机图形学和三维建模领域,3D旋转命令是实现物体空间变换的核心操作之一,它通过数学方法定义物体绕特定轴或点的角度变化,从而在二维屏幕上模拟三维空间的动态效果,3D旋转不仅广泛应用于游戏开发、动画制作、工业设计等领域,也是CAD软件、虚拟现实系统中的基础功能,理解3D旋转的原理、实现方式及应用场景,对于掌握三维图形编程至关重要。

3D旋转的基本原理
3D旋转的本质是在三维笛卡尔坐标系中,通过旋转矩阵或四元数等数学工具,改变物体上各顶点的坐标位置,与二维旋转不同,三维旋转需要明确旋转轴(如X轴、Y轴、Z轴或任意自定义轴)和旋转方向(顺时针或逆时针),根据欧拉旋转定理,任何三维旋转都可以通过绕某个固定轴的单一旋转来实现,但实际应用中常通过绕三个坐标轴的连续旋转(如ZYX顺序)来描述复杂旋转,这种方式称为欧拉角表示法。
3D旋转的实现方式
旋转矩阵法
旋转矩阵是3D旋转最直接的数学表达形式,通过一个3×3的正交矩阵与顶点坐标向量相乘,实现坐标变换,绕Z轴旋转θ角的旋转矩阵为:
[cosθ -sinθ 0]
[sinθ cosθ 0]
[ 0 0 1]绕X轴和Y轴的旋转矩阵类似,仅需调整对应轴的三角函数位置,当需要绕任意轴(如向量u=(ux,uy,uz))旋转时,需使用罗德里格斯旋转公式构造复合旋转矩阵,该方法计算量较大但通用性强,旋转矩阵的优点是计算效率高,适合GPU并行计算;缺点是存在万向节锁问题(欧拉角表示法中),且多次旋转时矩阵累积可能导致精度损失。
四元数法
四元数是一种扩展的复数形式,由一个实部和三个虚部(i,j,k)组成,表示为q=w+xi+yj+zk,在3D旋转中,单位四元数(满足w²+x²+y²+z²=1)可表示任意旋转,其优势在于避免了万向节锁问题,且插值计算(如球面线性插值SLERP)更平滑,四元数与旋转矩阵可相互转换,将四元数q转换为旋转矩阵的公式为:
[1-2y²-2z² 2xy-2wz 2xz+2wy ]
[ 2xy+2wz 1-2x²-2z² 2yz-2wx ]
[ 2xz-2wy 2yz+2wx 1-2x²-2y² ]四元数特别适合动画和游戏引擎中的角色旋转,因其存储空间小(仅需4个浮点数)、计算效率高且插值自然。
欧拉角表示法
欧拉角通过绕三个坐标轴(如XYZ、ZYX等顺序)的连续旋转来描述物体的姿态,其优点是直观易懂,便于用户交互(如通过鼠标拖拽调整旋转角度),欧拉角存在以下缺点:
- 万向节锁:当旋转至某一特定角度(如绕Y轴旋转90°)时,两个旋转轴重合,导致一个自由度丢失,无法通过欧拉角表示所有旋转。
- 旋转顺序依赖:不同旋转顺序(如XYZ与XZY)会导致完全不同的旋转结果,需根据应用场景明确约定顺序。
3D旋转的命令与API实现
在不同开发框架和软件中,3D旋转命令的语法和实现方式各异,以下是常见工具中的示例:
OpenGL中的旋转命令
OpenGL使用glRotatef(angle, x, y, z)函数实现旋转,其中angle为旋转角度(度),(x,y,z)为旋转轴向量,绕Y轴旋转30°的代码为:

glRotatef(30.0f, 0.0f, 1.0f, 0.0f);
该函数内部会生成对应的旋转矩阵,并与当前模型视图矩阵相乘,需要注意的是,OpenGL采用列主序矩阵,且旋转方向遵循右手定则(拇指指向旋转轴正方向,四指弯曲方向为旋转正方向)。
Unity引擎中的旋转
Unity引擎提供了多种旋转操作方式,包括欧拉角、四元数和旋转矩阵,通过Transform组件实现物体旋转:
// 使用欧拉角旋转(每帧绕Y轴旋转1度) transform.Rotate(0, 1, 0); // 使用四元数设置旋转(绕(1,1,1)轴旋转45度) Vector3 axis = new Vector3(1, 1, 1).normalized; transform.rotation = Quaternion.AngleAxis(45, axis);
Unity的Quaternion类封装了四元数运算,提供了EulerAngles属性用于欧拉角与四元数的相互转换,并内置了Slerp方法实现平滑插值。
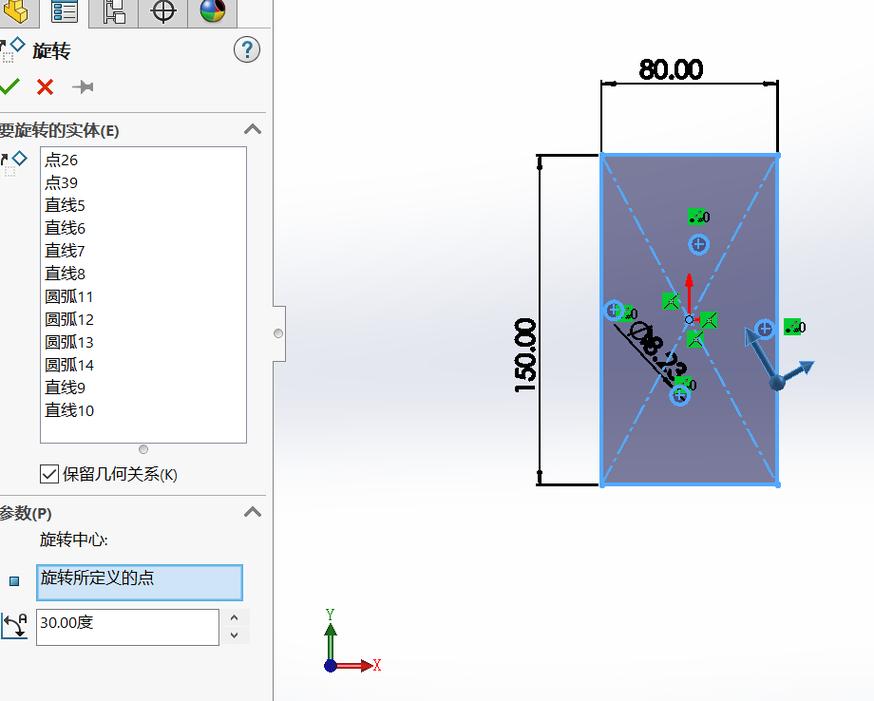
Blender中的旋转操作
Blender作为三维建模软件,支持多种旋转模式:
- 欧拉角旋转:在“旋转”面板中手动输入X、Y、Z轴角度,或使用
R键配合轴向快捷键(如RZ表示绕Z轴旋转)。 - 四元数旋转:在“变换”面板中切换为“四元数”模式,直接调整四元数数值。
- 轨道旋转:使用鼠标中键拖拽实现视图的轨道旋转(不改变物体自身旋转)。
3D旋转的应用场景
- 游戏开发:控制角色朝向、相机视角、物体动画等,如通过四元数插值实现角色头部平滑转动。
- 工业设计:在CAD软件中旋转零件进行装配检查,或通过3D旋转命令生成复杂曲面(如旋转扫描)。
- 医学影像:对CT、MRI扫描数据进行三维重建后,通过旋转操作多角度观察病灶。
- 虚拟现实:通过头部旋转追踪更新用户视角,实现沉浸式体验。
常见旋转问题与解决方案
旋转顺序与万向节锁
当使用欧拉角时,需避免万向节锁问题,解决方案包括:
- 改用四元数或旋转矩阵表示旋转。
- 采用Tait-Bryan角(如XYZ顺序)并限制旋转范围(如-90°到90°)。
- 在动画关键帧处插入“旋转分解”操作,避免连续旋转导致锁死。
旋转插值的平滑性
在动画中,直接插值欧拉角会导致旋转路径不平滑(如“抖动”现象),推荐使用四元数的球面线性插值(SLERP)或旋转矩阵的线性插值(LERP)后归一化,确保旋转轴和角度的连续变化。
相关问答FAQs
Q1: 为什么3D旋转中四元数比欧拉角更受欢迎?
A1: 四元数相比欧拉角具有以下优势:① 避免万向节锁问题,可表示任意旋转;② 存储空间更小(4个浮点数vs 3个),计算效率更高;③ 旋转插值(如SLERP)结果更平滑,适合动画和游戏中的角色旋转,欧拉角虽直观,但受限于旋转顺序和万向节锁,在复杂旋转场景中应用受限。
Q2: 如何在OpenGL中实现绕任意轴的旋转?
A2: 在OpenGL中,可通过glRotatef(angle, x, y, z)函数直接绕任意轴旋转,其中(x,y,z)为旋转轴的单位向量,若未归一化,OpenGL会自动进行归一化处理,绕向量(1,1,1)旋转45°的代码为:
glRotatef(45.0f, 1.0f, 1.0f, 1.0f);
也可手动构造罗德里格斯旋转矩阵,再通过glMultMatrixf()加载矩阵实现自定义旋转。