在工程仿真中,ANSYS作为主流的有限元分析软件,其命令流(APDL)功能允许用户通过编程方式实现复杂模型的参数化建模与求解,以悬臂梁分析为例,命令流的高效性和可重复性优势尤为突出,悬臂梁作为典型的力学模型,常用于验证软件功能或教学演示,其命令流编写需涵盖几何建模、网格划分、边界约束、载荷施加及求解后处理等完整流程,以下将详细展开ANSYS悬臂梁命令流的具体实现步骤及关键参数说明。
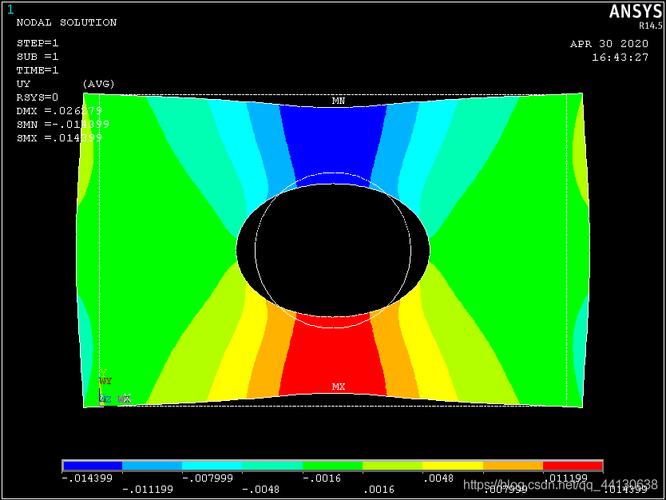
几何建模与材料属性定义
悬臂梁的几何建模通常通过关键点(K)和线(L)构建,参数化设计便于后续修改尺寸,假设梁长度为1m,截面为矩形,高度0.1m,宽度0.05m,命令流首先需定义关键点坐标,依次连接成线,材料属性方面,假设选用钢材,弹性模量取2.1e11Pa,泊松比0.3,密度7850kg/m³,可通过MP命令批量赋值。
/PREP7 ! 进入前处理器 /UNITS, SI ! 设置单位制为国际单位制 ! 定义材料参数 MP, EX, 1, 2.1e11 ! 弹性模量 MP, PRXY, 1, 0.3 ! 泊松比 MP, DENS, 1, 7850 ! 密度 ! 几何建模(参数化尺寸) L, 0.1, 0.05, 0 ! 矩形截面高度与宽度 /PNUM, LINE, 1 ! 显示线编号
此处通过参数化定义截面尺寸,若需调整模型,只需修改对应数值即可更新几何形状。
网格划分与单元选择
网格划分是影响计算精度的关键步骤,悬臂梁分析常选用Beam188单元(适合细长结构)或Solid185单元(三维实体),若采用Beam188单元,需先定义截面属性(SECTYPE, SECDATA),然后通过LMESH命令对线划分网格,网格密度控制可通过LESIZE命令设置单元长度,
! 选择单元类型 ET, 1, BEAM188 ! 梁单元 ! 定义截面属性 SECTYPE, 1, BEAM, RECT ! 矩形截面 SECDATA, 0.05, 0.1 ! 宽度、高度 ! 网格划分 LESIZE, ALL, 0.01, , , , , 1 ! 单元长度0.01m LMESH, ALL ! 对所有线划分网格
若使用Solid185单元,需先通过关键点生成面或体,再通过VMESH划分体网格,并需在截面处设置网格密度过渡,避免应力集中区域的误差。
边界约束与载荷施加
悬臂梁的边界条件为固定端(通常为梁的一端)完全约束,自由端施加集中力或均布载荷,固定端约束通过D命令施加,限制所有自由度(UX, UY, UZ, ROTX, ROTY, ROTZ);自由端载荷可通过F命令施加集中力,或SF命令施加压力,在自由端施加1000N向下的集中力:
! 施加约束(固定端:关键点1) D, 1, ALL, 0 ! 约束关键点1的所有自由度 ! 施加载荷(自由端:关键点2) F, 2, FY, -1000 ! 在Y方向施加-1000N集中力
求解与后处理
完成前处理设置后,通过/SOLU进入求解器,选择求解类型(静态分析),然后运行求解(SOLVE),求解完成后,进入后处理器(/POST1或/POST26),查看变形云图、应力分布及支反力等结果。
/SOLU ! 进入求解器 ANTYPE, STATIC ! 静态分析 SOLVE ! 求解 /POST1 ! 进入通用后处理器 PLDISP ! 显示变形云图 ! 查看应力分布 ETABLE, STRESS, SMISC, 1 ! 提取弯曲应力 PLETAB, STRESS ! 显示应力表
可通过参数化结果提取(如*GET命令)获取最大变形量或应力值,用于后续优化设计。
关键参数说明与注意事项
| 步骤 | 关键命令 | 参数说明 |
|---|---|---|
| 几何建模 | K, L | 关键点坐标、线连接方式,需确保尺寸单位与材料属性一致 |
| 材料属性 | MP, EX, PRXY | 弹性模量、泊松比需与实际材料匹配,若为复合材料需定义各向异性参数 |
| 网格划分 | ET, SECTYPE, LESIZE | 单元类型需符合分析需求(梁单元适合细长结构,实体单元适合复杂截面) |
| 边界约束 | D | 约束类型需与实际工况一致,避免过约束或欠约束 |
| 载荷施加 | F, SF | 集中力作用于节点,压力作用于面/线,需注意载荷方向与坐标系关系 |
相关问答FAQs
Q1:悬臂梁分析中,如何选择合适的单元类型(Beam188 vs Solid185)?
A1:选择单元类型需根据分析目的和几何特征决定,若梁的长度远大于截面尺寸(长细比>10),Beam188梁单元更高效,计算量小且结果准确;若需分析截面应力分布或复杂几何形状(如变截面、开孔),则应选用Solid185实体单元,能更真实模拟局部应力集中,但网格划分更复杂,计算耗时较长。

Q2:如何通过命令流验证悬臂梁理论解与仿真结果的一致性?
A2:可通过比较自由端挠度理论值与仿真结果验证,根据材料力学,悬臂梁自由端受集中力F时的挠度公式为δ=FL³/(3EI),其中L为长度,E为弹性模量,I为截面惯性矩,在命令流中提取最大变形量(如*GET, MAX_DEF, U, Y, MAX),与理论值对比,若误差较大,需检查网格密度(加密网格)、边界约束(是否完全固定)或材料参数(弹性模量是否正确)。