RSA加密算法是一种非对称加密算法,其安全性基于大数分解的数学难题,在RSA体系中,公钥和私钥是成对生成的,二者相互关联但无法通过其中一个轻易推导出另一个,以下是RSA公钥和私钥的详细生成过程,涉及数学原理、具体步骤及实际应用中的注意事项。
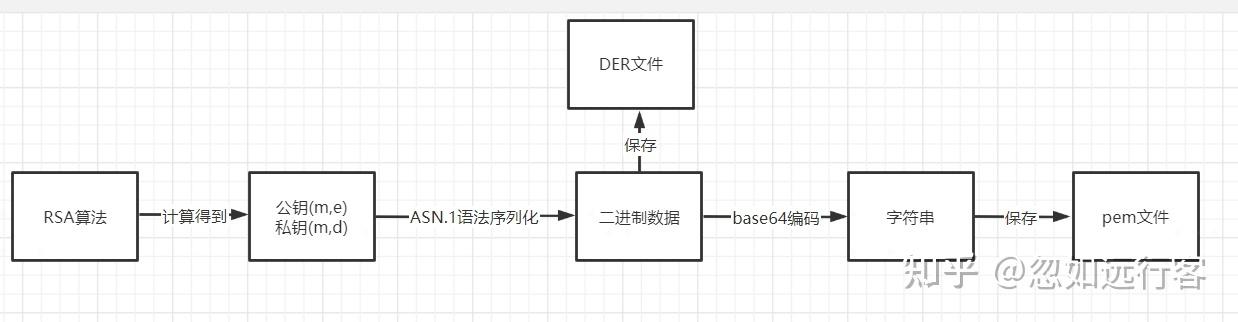
密钥生成的数学基础
RSA算法的核心是欧拉函数和模运算,选择两个大素数p和q(通常为1024位或2048位),计算其乘积n=p×q,n即为模数,欧拉函数φ(n)=(p-1)(q-1),用于计算与n互质的整数个数,密钥生成需满足以下条件:
- 选择一个整数e,满足1<e<φ(n)且e与φ(n)互质,e作为公钥的指数部分。
- 计算e关于φ(n)的模反元素d,即满足(e×d) mod φ(n)=1,d作为私钥的指数部分。
密钥生成步骤详解
选择大素数p和q
- 素数选择:通过概率性素数测试(如Miller-Rabin测试)生成两个大素数,确保其长度足够(如2048位),以抵抗因式分解攻击。
- 示例:假设p=61,q=53(实际应用中需远大于此值)。
计算模数n和欧拉函数φ(n)
- 模数n=p×q,示例中n=61×53=3233。
- 欧拉函数φ(n)=(p-1)(q-1)=60×52=3120。
生成公钥指数e
- e需满足与φ(n)互质且较小(通常选65537,因其为固定值且计算高效),示例中可选e=17(因gcd(17,3120)=1)。
计算私钥指数d
- 通过扩展欧几里得算法求解d=e⁻¹ mod φ(n),示例中,17×d ≡1 mod 3120,解得d=2753。
构造密钥对
- 公钥:(e, n),示例为(17, 3233)。
- 私钥:(d, n),示例为(2753, 3233),实际应用中私钥还需包含p和q等信息(如PKCS#1标准)。
密钥生成流程表
| 步骤 | 操作 | 数学公式/示例 | 说明 |
|---|---|---|---|
| 1 | 选择素数 | p=61, q=53 | 需大素数且保密 |
| 2 | 计算n和φ(n) | n=p×q=3233; φ(n)=(p-1)(q-1)=3120 | n公开,φ(n)保密 |
| 3 | 选择e | e=17 | 1<e<φ(n),gcd(e,φ(n))=1 |
| 4 | 计算d | d=e⁻¹ mod φ(n)=2753 | 私钥核心,需严格保密 |
| 5 | 输出密钥对 | 公钥(e,n); 私钥(d,n) | 公钥分发,私钥存储 |
实际应用中的注意事项
- 素数生成:需使用安全的随机数生成器(如/dev/urandom),避免弱素数导致漏洞。
- 密钥长度:当前推荐2048位以上,1024位已不安全。
- 私钥保护:私钥需加密存储(如使用AES算法),防止泄露。
- 标准化:遵循PKCS#1、RFC8017等标准,确保兼容性。
相关问答FAQs
Q1: 为什么RSA公钥中的e通常选择65537?
A1: 65537(2¹⁶+1)是一个固定值,其二进制形式为10000000000000001,仅需16次模乘即可完成加密,计算效率高,同时作为固定素数,可有效避免某些针对e的攻击(如e=3时的广播攻击)。
Q2: 如果RSA的私钥泄露,但公钥未变,是否需要重新生成密钥对?
A2: 是的,私钥泄露意味着攻击者可解密所有用该私钥加密的信息或伪造签名,即使公钥未变,也需立即生成新的密钥对,并吊销旧公钥的证书(如通过证书吊销列表CRL或OCSP),公钥的更新需通过安全渠道通知所有相关方。