如何难简易，是许多学习者在面对数学问题时常常需要掌握的技能，所谓“难简易”，并非单纯地将题目简化，而是通过分析题目结构、识别核心考点、合理拆解问题，从而将复杂问题转化为可解决的小步骤，这一过程需要结合数学知识、逻辑思维和一定的解题技巧,以下将从多个角度详细阐述如何实现数学题目的难简易转换。

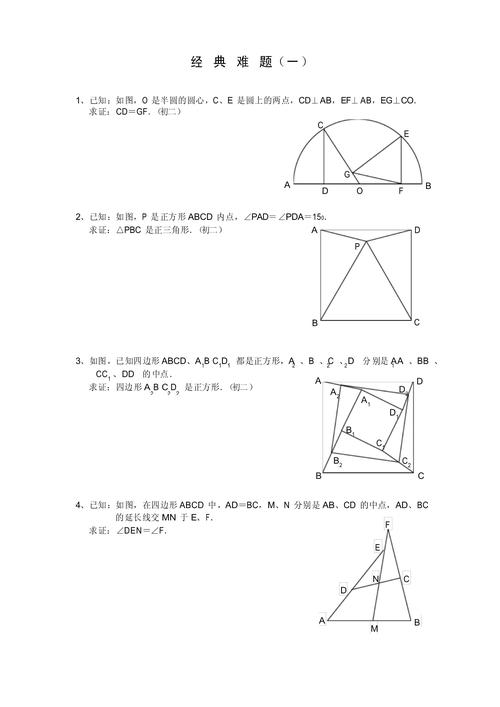
理解题意是难简易的第一步，许多数学题目看似复杂，往往是因为题干信息量大、条件隐蔽或表述抽象，需要耐心阅读题目，圈出关键数据、条件和问题目标，在应用题中，明确哪些是已知量，哪些是未知量，以及它们之间的关系，如果题目涉及多个变量，可以尝试用字母表示未知数，建立方程或表达式，这一过程相当于将文字信息转化为数学语言，为后续解题铺平道路，若题目中包含图形或图表，应先观察其特征，标注已知角度、长度或数量关系，直观的图形往往能帮助快速理解题意。 类型和核心考点是简化问题的关键，数学题目通常有固定的解题模式，如代数题中的因式分解、方程求解，几何题中的全等证明、面积计算，概率题中的事件分析等，通过快速判断题目类型，可以调用相应的解题方法和公式，遇到二次函数最值问题，若能识别出其顶点公式或配方法，便能直接套用，避免复杂的计算，对于综合性较强的题目，可以将其拆解为若干个单一知识模块的小问题，逐一攻克，一道结合了函数与几何的题目，可以先分析函数性质，再利用几何性质建立联系，这样化整为零,难度自然降低。

合理运用数学思想方法能显著提升解题效率，数学思想是解题的灵魂，如数形结合、分类讨论、转化与化归等，数形结合思想在代数和几何问题中尤为实用，例如用函数图像理解方程根的分布，或用几何模型解释代数表达式，分类讨论则适用于存在多种可能性的问题，如含绝对值的方程、参数取值影响结果的情况，通过分情况讨论，避免遗漏，转化与化归思想的核心是将未知问题转化为已知问题，例如将分式方程转化为整式方程，将复杂图形转化为基本图形，特殊化与一般化思想也很有帮助，对于抽象问题，可以先代入特殊值（如0、1）进行试探，寻找规律；对于具体问题，可以尝试总结一般性结论,便于举一反三。

在解题过程中，简化计算和步骤也是难简易的重要体现，复杂的计算往往容易出错，因此可以尝试寻找更简便的计算路径，利用运算律简化算式，或通过整体代入减少重复计算，在几何证明中，辅助线的添加是简化问题的关键，合理的辅助线能将分散的条件集中，或将复杂图形转化为简单图形，检查和验证也不可忽视，解出答案后，可以将其代入原题检验，或通过不同方法验证结果,确保正确性。

以下通过一个表格对比不同类型数学题目的难简易策略： 类型 | 难点分析 | 简化策略 | |----------------|---------------------------|--------------------------------------------------------------------------| | 应用题 | 文字信息量大，关系复杂 | 提取关键数据，设未知数，建立方程；画示意图辅助理解。 | | 几何证明题 | 条件分散，思路难找 | 添加辅助线，将图形分解；利用全等、相似等性质转化问题。 | | 函数综合题 | 涉及多个知识点，计算繁琐 | 分模块分析函数性质（单调性、最值），结合方程或不等式求解。 | | 概率统计题 | 情境抽象，事件关系复杂 | 列举所有可能结果，明确事件类型；用树状图或表格辅助分析。 |

培养良好的解题习惯和思维能力是长期提升难简易能力的基础，平时练习时，应注重一题多解和错题反思，通过多种解法比较最优路径，通过错题分析错误原因，避免重复失误，多总结解题规律和技巧，形成自己的知识体系,才能在遇到新题目时快速找到突破口。

相关问答FAQs：

Q1：如何应对自己完全没见过的数学题型？
A1：遇到陌生题型时，首先不要慌张，仔细阅读题目，尝试提取已知条件和问题目标，然后联想相关知识模块，看是否能将其转化为熟悉的问题类型，若题目涉及新的定义或符号，可先理解其含义，再通过举例或画图帮助理解，尝试从简单情况入手，代入特殊值或简化条件，寻找规律,逐步推导一般解法。

Q2：数学题目计算过程太复杂，如何减少错误？
A2：减少计算错误可从两方面入手：一是简化计算步骤，尽量使用运算律、公式或整体代入等方法，避免繁琐的中间计算；二是规范书写过程，清晰标注每一步的依据，便于检查，完成后，可通过逆向代入、估算或不同方法验证结果，确保答案的准确性，平时练习时注意培养心算和速算能力,也能提高计算效率。