相向追击问题是一类典型的运动学问题,其核心在于分析两个物体在运动过程中的位置关系,通过建立方程求解速度,解决这类问题需要明确运动方向、时间关系和位移关系,以下是详细的解题思路和方法。

要明确“相向”和“追击”的含义,相向运动指两个物体相向而行,即运动方向相反;追击运动指两个物体同向运动,后者试图追上前者,在相向追击问题中,通常涉及两个物体的初始距离、速度、运动时间以及相遇或追及时的条件,解题的关键步骤如下:
第一步,明确研究对象和运动过程,确定两个物体的运动性质(匀速、匀变速等)和运动方向,这是建立方程的基础,若两物体相向而行,则它们的相对速度为速度之和;若同向追击,则相对速度为速度之差(假设追击者速度大于被追击者)。
第二步,设定变量并统一单位,通常设两物体的速度分别为( v_1 )和( v_2 ),运动时间为( t ),初始距离为( s_0 ),需注意将所有物理量统一为国际单位制(如米、秒、米/秒),避免单位混淆。
第三步,分析位移关系并建立方程,根据运动方向和相遇/追击条件,列出位移方程,以下是常见情况的位移关系总结:
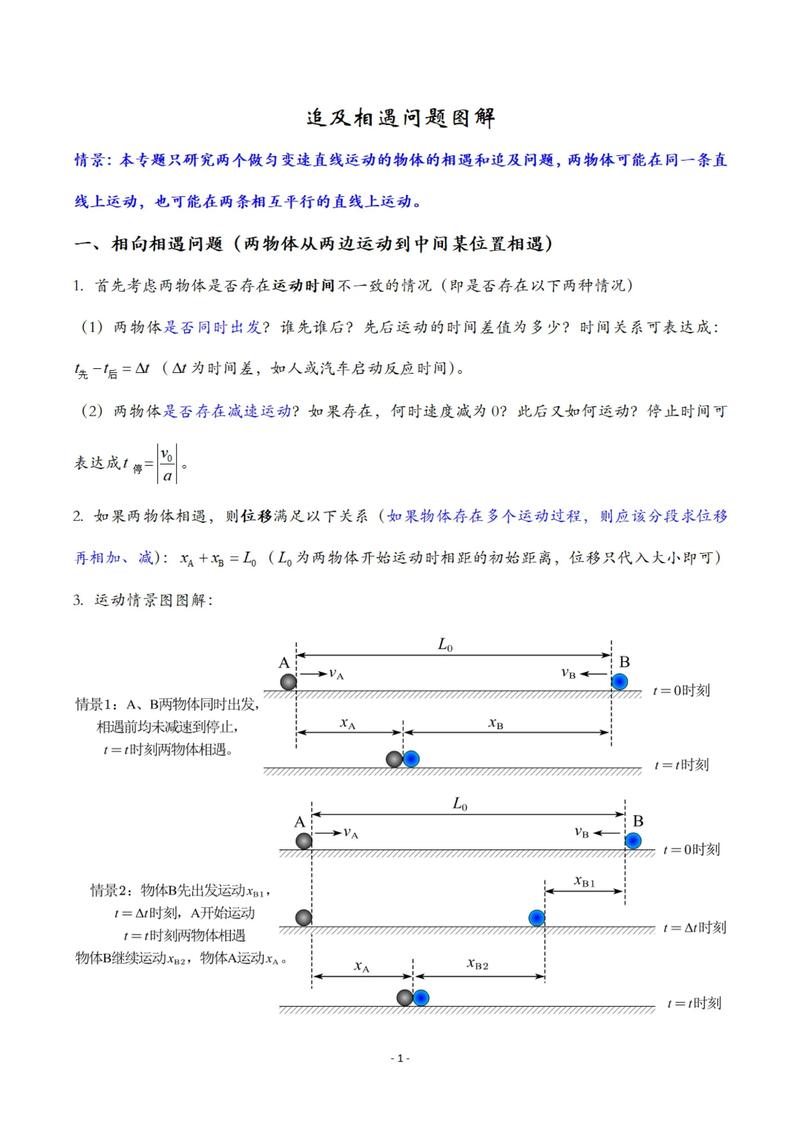
| 运动类型 | 位移关系方程 | 相对速度 |
|---|---|---|
| 相向而行 | ( s_1 + s_2 = s_0 )(( s_1 = v_1 t ), ( s_2 = v_2 t )) | ( v_1 + v_2 ) |
| 同向追击 | ( s_1 - s_2 = s_0 )(( s_1 = v_1 t ), ( s_2 = v_2 t ), ( v_1 > v_2 )) | ( v_1 - v_2 ) |
| 相向而行且有加速度 | ( s_1 = v_1 t + \frac{1}{2}a_1 t^2 ), ( s_2 = v_2 t + \frac{1}{2}a_2 t^2 ), ( s_1 + s_2 = s_0 ) | 需通过加速度计算 |
第四步,代入已知条件求解未知量,根据题目给出的条件(如相遇时间、追及条件等),将已知数值代入方程,解方程求出未知速度或时间,若已知两物体相向而行,初始距离为100米,甲速度为5米/秒,乙速度为3米/秒,则相遇时间( t = \frac{s_0}{v_1 + v_2} = \frac{100}{5+3} = 12.5 )秒。
第五步,验证结果合理性,求解后需检查结果是否符合物理实际,如速度是否为正、时间是否为正、追击问题中追击者速度是否大于被追击者等,若出现负值或矛盾结果,需重新检查方程建立过程或已知条件是否正确。
在复杂问题中,可能涉及多个阶段或不同运动状态,此时需分段分析,两物体先相向运动,相遇后其中一物体反向运动,需分别计算相遇前后的位移和时间关系,并注意衔接点的速度和位置条件。
利用相对运动思想可简化问题,以地面为参考系时,两物体的运动需分别计算;若以其中一个物体为参考系,则另一物体的相对速度可直接用于计算,同向追击时,以被追击者为参考系,追击者的相对速度为( v_1 - v_2 ),初始距离为( s_0 ),则追及时间( t = \frac{s_0}{v_1 - v_2} ),这种方法减少了变量数量,简化了计算。

需要注意的是,若物体做匀变速运动,需引入加速度变量,并利用匀变速运动公式(如( v = v_0 + at ), ( s = v_0 t + \frac{1}{2}at^2 ))建立方程,此时方程可能为二次方程,需通过求根公式求解,并结合物理意义舍去不合理解。
解决相向追击问题的核心是:明确运动方向、建立正确的位移关系方程、统一单位、合理求解并验证结果,通过系统分析和方法总结,此类问题可转化为数学方程求解,关键在于对物理过程的准确理解和数学工具的灵活应用。
相关问答FAQs:
-
问:在相向追击问题中,如何判断是否需要考虑加速度的影响?
答:若题目中明确说明物体做匀速直线运动,则无需考虑加速度;若提到“匀加速”“匀减速”或给出加速度数值,则需引入加速度变量,使用匀变速运动公式建立方程,若两物体相向匀加速运动,则位移方程需包含加速度项( \frac{1}{2}at^2 ),此时方程可能为二次方程,需结合时间、速度的物理意义求解。 -
问:当两物体相遇后,其中一物体反向运动,如何计算此时的速度关系?
答:相遇后物体的运动方向改变,需重新分析运动过程,首先计算相遇时的位置和时间,然后根据新的运动方向建立位移方程,甲、乙两物体相向而行相遇后,乙反向以原速运动,此时甲继续前行,乙反向运动,需以相遇点为新的起点,分别计算两者的位移关系(如甲的位移减去乙的反向位移等于后续条件中的距离),关键在于分段处理,明确各阶段的运动方向和初始条件。