在长方形内绘制椭圆是一个常见的几何作图需求,尤其在工程制图、设计或数学教学中较为常见,要准确完成这一操作,需结合几何原理和实用工具,以下是详细的方法步骤和注意事项。

基本原理
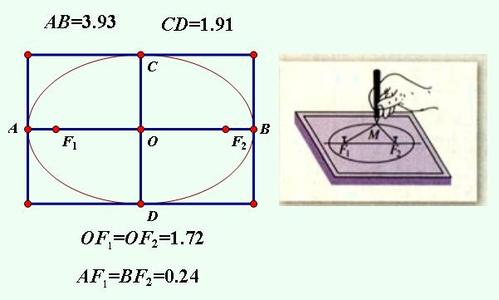
椭圆是平面上到两定点(焦点)距离之和为常数的点的轨迹,在长方形内绘制椭圆,通常指绘制一个与长方形四边相切的内切椭圆,此时椭圆的长轴与长方形的长边平行,短轴与长边垂直,这种椭圆也称为“长方形的内切椭圆”,其中心与长方形的中心重合,长轴长度等于长方形的长度,短轴长度等于长方形的宽度。
绘制工具与材料
- 绘图工具:直尺、圆规、铅笔、橡皮、绘图板(可选)。
- 辅助工具:三角板(用于确保直角)、量角器(可选,用于精确角度测量)。
- 数字化工具:若使用计算机绘图软件(如AutoCAD、Illustrator、GeoGebra等),可通过输入长方形尺寸直接生成内切椭圆。
手工绘制步骤(以长方形ABCD为例,AB为长边,AD为短边)
确定长方形中心
- 用直尺连接长方形对角线AC和BD,两对角线的交点O即为长方形的中心,也是椭圆的中心。
- 标记中心点O,并过O作长边AB和短边AD的平行线,得到椭圆的长轴和短轴方向。
确定椭圆长轴和短轴端点
- 长轴端点:在长边AB和CD上,分别以O为中心,向两侧量取长度的一半(即AB/2),得到长轴端点E、F(E在AB上,F在CD上)。
- 短轴端点:在短边AD和BC上,分别以O为中心,向两侧量取宽度的一半(即AD/2),得到短轴端点G、H(G在AD上,H在BC上)。
使用圆规绘制椭圆(近似法)
由于椭圆不是圆,无法直接用圆规绘制,但可通过“四心法”绘制近似椭圆:
- 步骤1:连接长轴端点E、F和短轴端点G、H。
- 步骤2:以O为中心,以OE为半径画弧,与短轴GH的延长线交于点K。
- 步骤3:以G为中心,以GK为半径画弧,与EF交于点L。
- 步骤4:以L为中心,以LE为半径画弧,与EF交于点M。
- 步骤5:连接KM,以KM为对称轴,分别在四段弧线上取对称点,最终通过平滑连接各点得到近似椭圆。
注意:四心法绘制的椭圆为近似值,若需更高精度,可增加更多辅助点或使用曲线板。
使用曲线板绘制精确椭圆
- 步骤1:在长方形内标记长轴和短轴端点E、F、G、H。
- 步骤2:通过这些点,用曲线板分段绘制平滑曲线,确保曲线对称且通过所有端点。
- 步骤3:绘制时,曲线板需与已绘制的部分重合一部分,以保证曲线连续。
数字化绘制方法(以GeoGebra为例)
- 打开GeoGebra,选择“几何”视图。
- 使用“多边形”工具绘制长方形ABCD,输入坐标或直接拖拽确定顶点。
- 找到长方形中心O(可通过“中点”工具或对角线交点确定)。
- 使用“椭圆”工具,依次选择长轴端点E、F和短轴端点G、H,软件自动生成内切椭圆。
注意事项
- 尺寸准确性:手工绘制时需确保长方形各边长度和中心点位置的准确性,否则椭圆会发生形变。
- 曲线平滑度:使用曲线板时,分段长度不宜过大,否则曲线可能不平滑。
- 比例选择:若长方形长宽比过大(如长度远大于宽度),椭圆会显得扁平,需确认是否为预期效果。
常见问题与解决方法
以下是绘制过程中可能遇到的常见问题及解答:
Q1:为什么用圆规直接画出的椭圆形状不对称?
A:圆规只能画圆,无法直接画椭圆,若尝试用圆规通过移动半径绘制,会导致椭圆不对称,需采用四心法或曲线板,确保长轴和短轴的端点位置准确,并通过对称方式分段绘制。
Q2:数字化软件中无法生成内切椭圆,是什么原因?
A:可能是软件操作步骤错误,在GeoGebra中绘制椭圆时,需依次选择长轴的两个端点和短轴的一个端点,而非随意选择三个点,需确认长方形的尺寸输入正确,且椭圆工具选择的是“给定两轴端点”模式而非“焦点”模式,若仍有问题,可参考软件帮助文档或教程重新操作。