证明“将军饮马”问题中的路径最短,需要借助数学中的对称原理和两点之间线段最短的公理,以下是详细的证明过程:
问题模型与对称转化
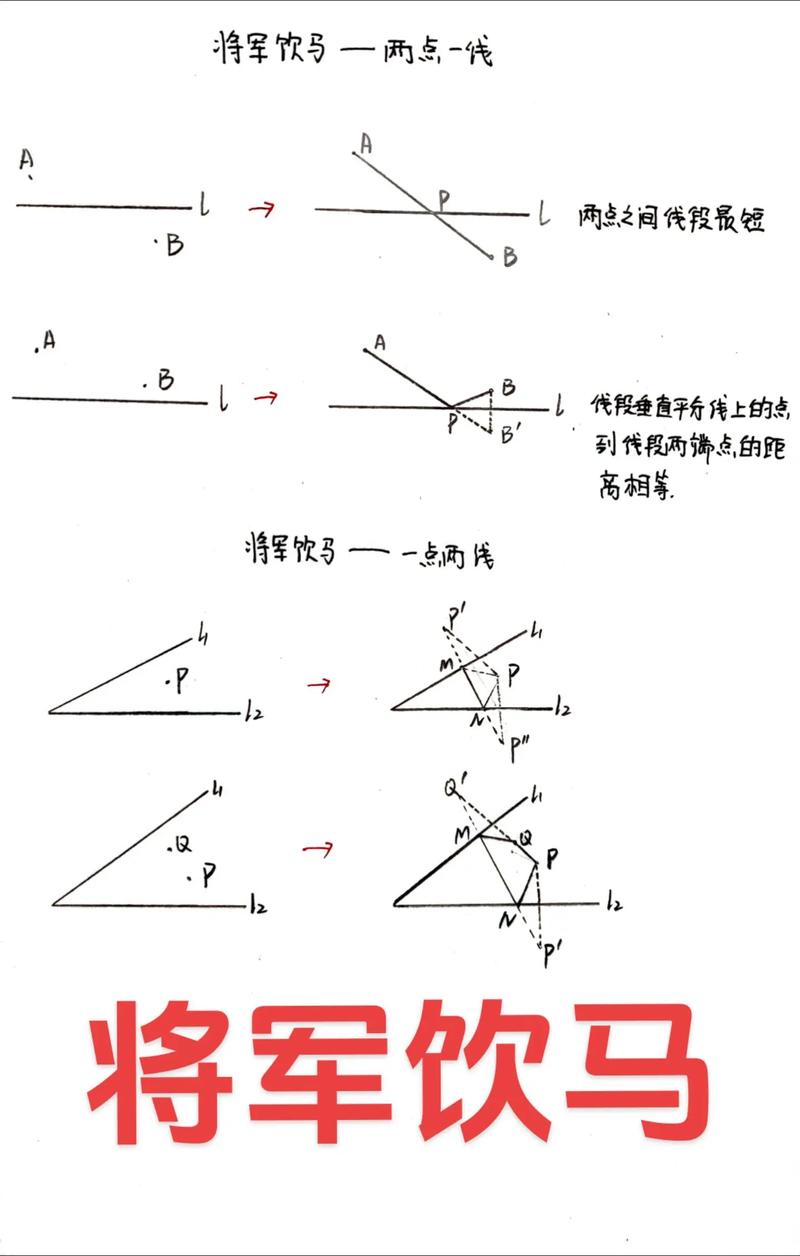
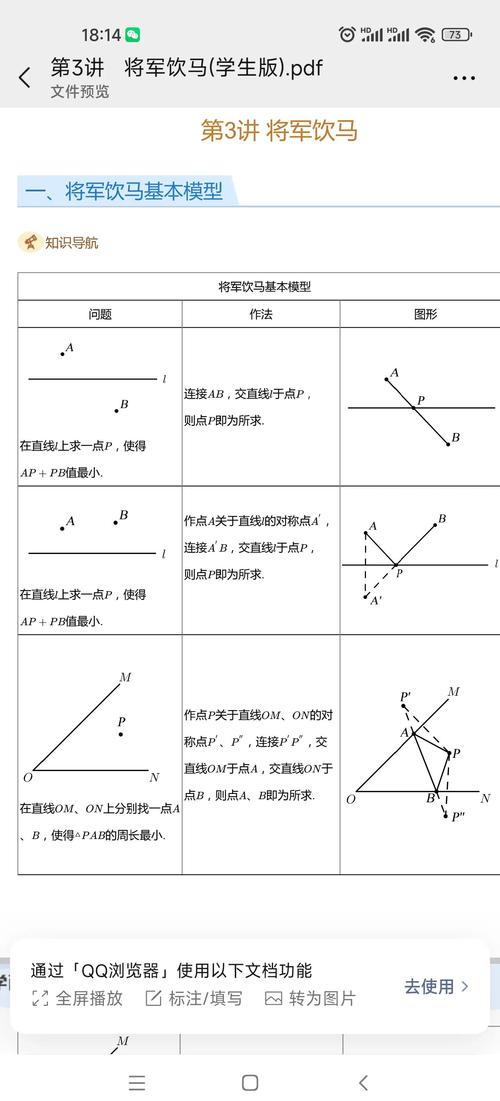
“将军饮马”问题可抽象为:在直线 ( l ) 的两侧有两点 ( A ) 和 ( B ),将军从 ( A ) 出发,必须到河边(直线 ( l ))饮马后再到 ( B ),求使路径 ( A \to P \to B ) 最短的点 ( P ) 的位置。
证明核心步骤:
- 作对称点:作点 ( A ) 关于直线 ( l ) 的对称点 ( A' )。
- 连接线段:连接 ( A'B ) 与直线 ( l ) 的交点即为所求点 ( P )。
证明路径最短
根据对称性,( AP = A'P ),因此路径 ( APB ) 的长度等于 ( A'PB )。
- 公理应用:两点之间线段最短,故 ( A'B ) 是 ( A' ) 到 ( B ) 的最短路径。
- 唯一性:若存在另一点 ( Q ) 在 ( l ) 上,则 ( AQ + QB = A'Q + QB ),由于 ( A'Q + QB \geq A'B )(三角形两边之和大于第三边),仅当 ( Q ) 与 ( P ) 重合时取等号。
( P ) 点使路径 ( APB ) 最短,且路径长度为 ( A'B ) 的长度。
数学验证(表格对比)
| 路径方案 | 路径长度表达式 | 最短性证明 |
|---|---|---|
| ( APB )(对称法) | ( A'B ) | 线段最短,无更优解 |
| 任意点 ( Q ) | ( A'Q + QB ) | ( A'Q + QB > A'B )(( Q \neq P )) |
几何直观解释
通过对称转化,将军从 ( A ) 到 ( B ) 的路径被转化为从 ( A' ) 直接到 ( B ) 的路径,由于对称不改变距离,且直线是两点间的最短路径,( P ) 点必然满足最短条件。
FAQs
问题1:为什么对称法能保证路径最短?
解答:对称法将折线问题转化为直线问题,根据对称性,( AP = A'P ),因此路径 ( APB ) 的长度等于 ( A'PB ),而两点之间线段最短,故 ( A'B ) 是最短路径,其与 ( l ) 的交点 ( P ) 即为最优解。
问题2:如果将军必须在河岸上行走一段固定距离,如何调整解法?
解答:若需在河岸上行走固定距离(如 ( PQ = d )),可将问题转化为:在 ( l ) 上找点 ( P )、( Q ) 使 ( PQ = d ),且 ( AP + PQ + QB ) 最短,此时需先平移 ( B ) 到 ( B' )(使 ( BB' \parallel l ) 且 ( BB' = d )),再作 ( A ) ( l ) 的对称点 ( A' ),连接 ( A'B' ) 与 ( l ) 的交点即为 ( P ),( Q ) 为 ( P ) 沿 ( l ) 方向移动 ( d ) 后的点。











