分数应用题是小学数学学习中的重点和难点,许多学生在解题时容易感到困惑,常常因为找不到解题思路或对分数意义理解不透彻而出错,要突破分数应用题这一关,需要从理解概念、掌握方法、多加练习等多个方面入手,逐步建立解题的思维模式。

深刻理解分数的意义是突破分数应用题的基础,分数不仅可以表示“部分与整体的关系”,如“把一个蛋糕平均分成8份,吃掉了3份,吃了这个蛋糕的3/8”;还可以表示“两个量之间的比较关系”,即“一个量是另一个量的几分之几”,男生人数是女生的4/5”,在解题时,首先要明确题目中分数的具体含义,是表示“部分量占总量的几分之几”,还是表示“一个量是另一个量的几分之几”,对于“部分与整体”的关系,通常把整体看作单位“1”,对应的量用“1”表示;对于“两个量比较”的关系,要弄清谁是单位“1”的量,谁是与之比较的量。“一根绳子长10米,用去了1/4”,这里的1/4表示“用去的长度占绳子总长度的1/4”,总长度10米是单位“1”;而“用去的长度是剩下长度的1/4”,则剩下长度是单位“1”,只有准确把握单位“1”,才能正确分析数量关系。
掌握分数应用题的基本类型和对应的关系式是解题的关键,分数应用题通常分为三类:求一个数的几分之几是多少、已知一个数的几分之几是多少求这个数、求一个数是另一个数的几分之几,这三类问题分别对应乘法、除法和除法(或分数减法)的关系式。
第一类,“求一个数的几分之几是多少”,用乘法计算,关系式:单位“1”的量 × 分率 = 对应的量。“六年级有学生200人,其中男生占3/5,男生有多少人?”这里单位“1”的量是六年级总人数200人,分率是3/5,求男生人数(对应的量),用乘法计算:200 × 3/5 = 120(人),解题时,要找准单位“1”的量和所求量对应的分率,直接用乘法列式。
第二类,“已知一个数的几分之几是多少求这个数”,用除法计算,也可以用方程解,关系式:对应的量 ÷ 分率 = 单位“1”的量。“一本书看了60页,正好是全书的3/5,全书有多少页?”这里“60页”是“对应的量”,“3/5”是分率,单位“1”的量是全书页数(未知),用除法计算:60 ÷ 3/5 = 100(页),用方程解时,设单位“1”的量为未知数x,根据“单位‘1’的量 × 分率 = 对应的量”列方程,如x × 3/5 = 60,解得x = 100,这类问题的关键是逆向思考,从已知量和分率推出单位“1”的量。

第三类,“求一个数是另一个数的几分之几”,用除法计算,关系式:一个数 ÷ 另一个数(单位“1”的量) = 分率。“小明家养了20只鸡,15只鸭,鸡的只数是鸭的几分之几?”这里鸭的只数是单位“1”的量,鸡的只数是比较的量,用鸡的只数除以鸭的只数:15 ÷ 20 = 3/4,解题时要明确“谁是谁的几分之几”,即找准被除数和除数,除数是单位“1”的量。
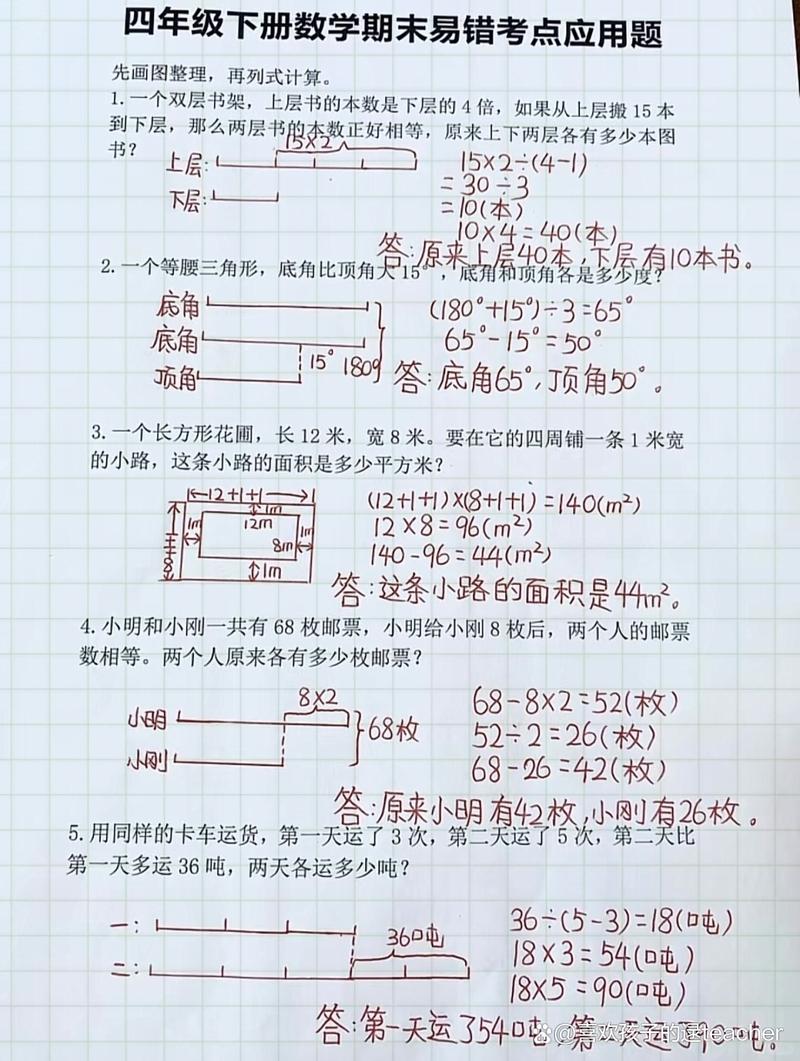
对于较复杂的分数应用题,如涉及两个或多个单位“1”,或包含“比多”“比少”等条件的题目,可以通过画线段图来帮助理解,线段图能直观地表示题目中的数量关系,把抽象的分数转化为具体的线段,便于找到等量关系。“一堆煤,第一次用去了全部的1/3,第二次用去了剩下的1/2,还剩12吨,这堆煤原有多少吨?”这道题有两个单位“1”,第一次的单位“1”是“全部煤”,第二次的单位“1”是“剩下的煤”,画线段图时,先画一条线段表示全部煤(单位“1”),第一次用去1/3,剩下2/3;再画一条表示剩下的煤(2/3),第二次用去剩下的1/2,即用去(2/3)×1/2=1/3,最后剩下的是2/3的1/2,即(2/3)×1/2=1/3,对应12吨,设这堆煤原有x吨,列方程x × (1 - 1/3) × (1 - 1/2) = 12,解得x = 36(吨),通过线段图,可以清晰地看到两次用煤后剩下的煤占总量的几分之几,从而顺利解题。
在解题过程中要注意单位的统一和答案的合理性,如果题目中涉及不同的单位,要先统一单位;计算后要检查答案是否符合生活实际,如人数不能是小数,长度不能为负数等,要多进行对比练习,区分易混淆的概念。“一根绳子截去1/4米”和“一根绳子截去全长的1/4”,前者是一个具体的数量(1/4米),后者是分率(全长的1/4),解题方法和结果完全不同,通过对比,可以加深对分数意义和数量关系的理解。
为了更好地掌握分数应用题的解题方法,可以按照以下步骤进行:第一步,认真审题,找出题目中的已知条件和所求问题;第二步,确定单位“1”的量,明确分数表示的意义;第三步,根据数量关系选择合适的解题方法(乘法、除法或方程);第四步,列式计算,注意运算顺序和计算准确性;第五步,检验答案,确保符合题意。
以下是分数应用题三类基本问题的对比表:
| 问题类型 | 数量关系 | 解题方法 | 示例 |
|---|---|---|---|
| 求一个数的几分之几是多少 | 单位“1”的量 × 分率 = 对应的量 | 乘法 | 六年级有学生200人,男生占3/5,男生有多少人?200 × 3/5 = 120(人) |
| 已知一个数的几分之几是多少求这个数 | 对应的量 ÷ 分率 = 单位“1”的量 | 除法或方程 | 一本书看了60页,是全书的3/5,全书有多少页?60 ÷ 3/5 = 100(页) |
| 求一个数是另一个数的几分之几 | 一个数 ÷ 另一个数(单位“1”)= 分率 | 除法 | 鸡15只,鸭20只,鸡是鸭的几分之几?15 ÷ 20 = 3/4 |
突破分数应用题需要坚持不懈的练习,通过练习,可以熟悉各种题型,掌握解题技巧,提高解题速度和准确率,练习时要注意精选题目,既要基础题,也要综合题,逐步提升解题能力,遇到难题时,要勇于思考,多与同学、老师交流,分析错误原因,总结解题经验,不断改进学习方法。
相关问答FAQs:
问题1:分数应用题中如何快速找到单位“1”?
解答:找单位“1”是解分数应用题的核心,单位“1”的量出现在“占”“是”“比”“相当于”等关键词后面的量。“男生占全班人数的3/5”,全班人数是单位“1”;“比原计划节约了1/6”,原计划是单位“1”,如果句子中没有明显的关键词,可以根据“部分与整体”的关系判断,整体通常是单位“1”;在“甲是乙的几分之几”中,乙是单位“1”,单位“1”的量在题目中有时是已知的,有时是未知的,需要根据问题来确定。
问题2:遇到复杂分数应用题(如多个单位“1”)时,如何拆解解题?
解答:复杂分数应用题可以通过“分步法”或“转化法”拆解,分步法:将题目分解成几个简单问题,逐步求解。“先求第一次操作后的剩余量,再以剩余量为单位‘1’求第二次操作后的量,最后根据剩余量与总量的关系列方程”,转化法:将多个单位“1”转化为统一的单位“1”。“甲是乙的1/2,乙是丙的1/3”,可以转化为“甲是丙的(1/2×1/3=1/6)”,以丙为单位“1”,画线段图是辅助拆解复杂问题的有效工具,通过线段图可以直观展示各量之间的关系,帮助理清思路,找到等量关系。